The software intelligence explosion debate needs experiments

Published

Nov 14, 2025

Authors

Suppose you had a million AIs, each surpassing humanity’s best AI researchers. If they all worked on advancing AI, how much would AI progress accelerate?

This might sound like science fiction, but it may be the most consequential question about the future of AI. The problem is that the experts disagree wildly on the answer.

Some foresee a positive feedback loop. These AIs are smart enough to find new algorithms to make smarter AIs, which make even smarter AIs, and so on. Very soon, we could see multiple years of AI progress compressed into a single year just through software advances — a “software intelligence explosion”.¹

Others agree that AI progress would speed up, but think that something will block the explosive feedback loop. For example, increasing difficulty in finding new algorithms might bottleneck AI self-improvement, or software improvements might depend heavily on physical resources like compute, which can’t be scaled as easily.

And we really need to know who’s right. If a software intelligence explosion is likely, economic and military power might become much more concentrated in a few companies or nations. They might also focus more on automating AI research rather than driving broad economic impacts — so AI progress could rapidly accelerate before most of the world knows what’s happening.

So why do the experts disagree so much, and how can we figure out who’s right?

Flawed data

The core reason for this disagreement is a lack of strong evidence — thus far, empirical work on the software intelligence explosion has used flawed data and models.

Prior work has used the “Jones model”, which tells us how R&D inputs translate into outputs. For example, the R&D input might be the number of AI researchers, and the R&D output could measure how efficiently an AI algorithm uses training compute (“software efficiency”).²

The core parameter in this model is the “returns to R&D” — in our example, this tells us how software efficiency changes when we double the number of researchers. If it also doubles, the returns are just 1. If it quadruples, then the returns are 2. In general, if doubling the inputs increases the output by $2^r$, then the returns are $r$.

This parameter dictates the long-run dynamics of the software intelligence explosion.³ We especially care if we have increasing returns (i.e. $r > 1$) — this is when you get more than what you put in, resulting in the positive feedback loop where smarter AIs recursively build smarter AIs.⁴ ⁵

So far, so good. But the issues show up when we apply this in practice. Consider our estimates of these returns in several domains of AI software:⁶

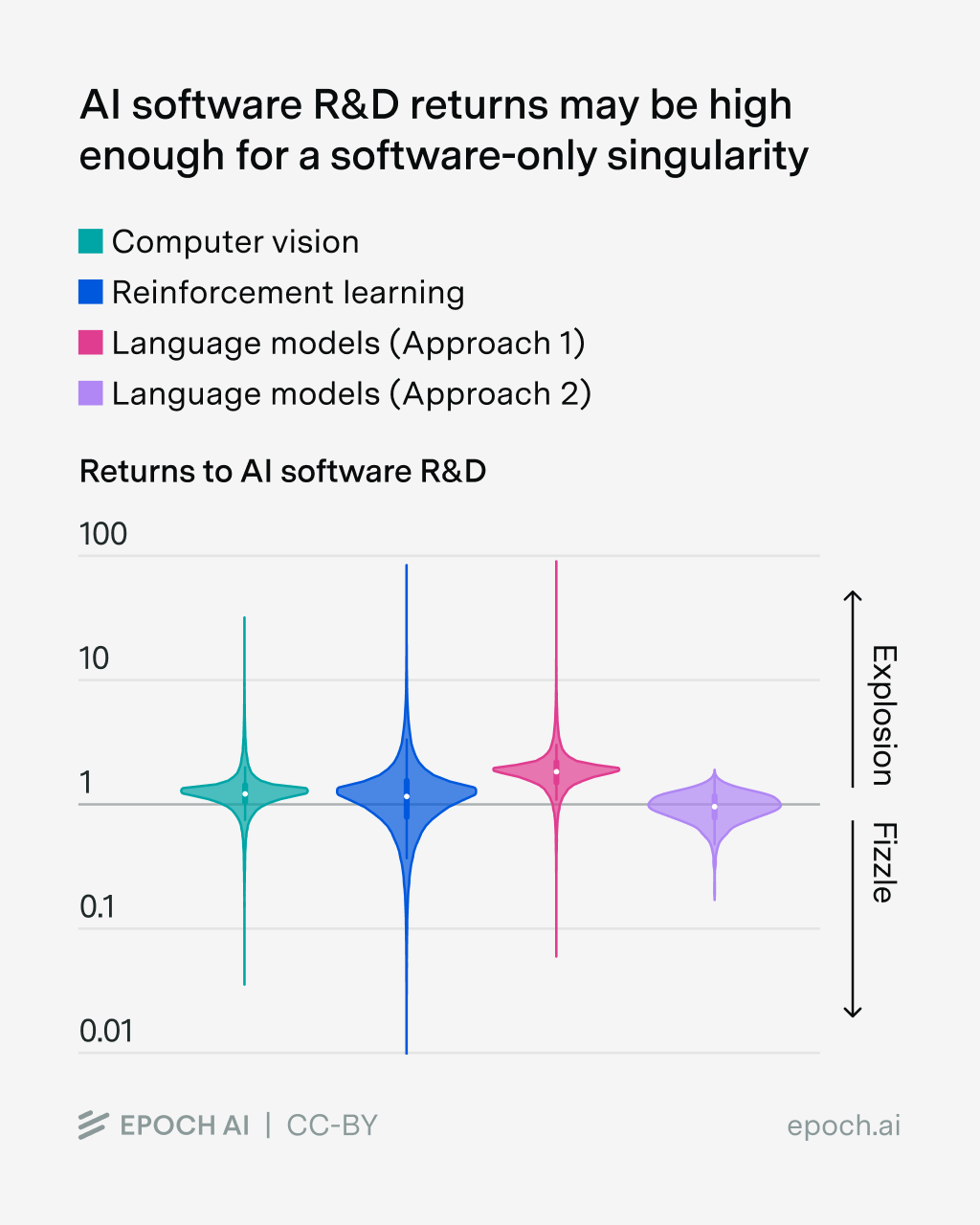
Estimates of the returns to software R&D for three different domains of AI: (1) computer vision, (2) reinforcement learning, and (3) language models. Technical details are provided in the appendix.

Here we see a lot of probability on compounding returns. But the uncertainty is very large, and our range of estimates straddle the key threshold of $r=1$. So at face value, the software intelligence explosion seems quite plausible — at the very least, it’s hard to rule out.

But if we dig into the details, we see a ton of big problems. To estimate $r$, we need to collect data on R&D inputs and outputs, but our measures of these are very imperfect.

For example, to estimate the returns in language models, we first looked at the number of published papers in natural language processing. This proxies for the number of researchers, accounting for how some researchers might be more productive than others (and hence publish more papers).

But this ignores all the R&D effort that spills over from other domains of AI. For example, it’s common for language models like the Transformer to use “residual connections”, but this innovation was heavily inspired by work in computer vision.

So we also considered a second measure of R&D inputs, which is a function of human labor and AI compute at AI labs. Unfortunately, this is flawed for a similar reason — it ignores the R&D effort that spills over from researchers outside of a collection of AI companies.⁷ For instance, OpenAI’s work is often inspired by academic research.

So these “spillover effects” cause a mismatch between R&D inputs and what we measure it to be. But it’s not clear how best to adjust for this — we could include papers from computer vision and other domains of AI, but many of these papers will be unrelated to language model improvements! We could also try to account for academic R&D inputs, but we don’t know how much academic research compute there was over time. In general, we don’t have good data on the inputs and need to rely on proxies or best-guesses with limited data.

What does this mean for our estimates of the returns to R&D? Possibly this means that the “true” returns should be higher than what we observe. In particular, both the number of researchers and supply of compute probably grows more slowly in academia compared to AI labs.⁸ So if we broaden our metric to include academia, we’d measure slower R&D input growth. This means fewer input doublings for the same number of output doublings, so the estimated returns to R&D become higher.

There are similar issues with the R&D outputs. Ideally we’d like to have a fine-grained measure of software quality over time, but unfortunately we only have an average growth rate. This forces us to make strong assumptions to get estimates — for instance, we assume that software progress has proceeded at a constant rate. This is plausibly consistent with existing empirical evidence, but we think the evidence on this is quite weak. In fact, the rise of reasoning models might’ve marked an acceleration in algorithmic progress.

In general, there are a whole host of data-related issues that we need to contend with when estimating these returns, which might bias our estimates upward or downward.⁹

Flawed models

Even without data issues, we might still end up with misleading estimates. The problem is that we’re taking the Jones model way beyond what has been empirically observed.

The model was originally written for the whole economy, where the main input, researchers, and the main output, productivity, are growing at a few percent a year. But we’re trying to apply to a situation where the inputs are growing by orders of magnitude in a few years — i.e. the software intelligence explosion, where you get many more AI workers that become increasingly intelligent. So we shouldn’t be too surprised if the Jones law of motion is pretty badly misspecified for thinking about the software intelligence explosion.

One issue is that finding software improvements might require running experiments close to the size of frontier training runs. This can make a huge difference — for instance, in previous empirical work, such compute requirements could prevent a software intelligence explosion.¹⁰ But some previous work neglects this dynamic.

Another issue is that the Jones model doesn’t include a hard limit on how much research can be parallelized at a given time.¹¹ So if you scale up the number of AI researchers really fast, the model predicts that software progress should go to infinity essentially immediately. But this seems implausible — you couldn’t get infinite software progress in five minutes even if you had infinitely many Alec Radfords doing AI research. You still need to run experiments and wait for them to finish, and some software innovations might need to happen in sequence. So if we naively apply the Jones model, we might vastly overstate how much software progress we see when AI R&D is automated.

Finally, when most people think of an intelligence explosion, they think of AIs getting smarter and smarter, but most models of the intelligence explosion consider making AI more and more numerous. It’s not clear that this is what people actually care about, as having infinite copies of GPT-2 would arguably have little impact on the world. The difficulty with modeling “intelligence” increases is that it’s not clear how intelligence translates into effective research input. Is being twice as smart as good as having twice as many researchers? We have fairly minimal data on this front, and adjusting for it has unclear implications. On the one hand, the returns to intelligence in R&D might be extremely high, effectively increasing $r$. On the other hand, if we changed the output of R&D to intelligence, this has plausibly grown much slower than effective compute, lowering $r$.

Part of the issue here is that we don’t know enough about the nature of algorithmic progress to know which model is right. This can lead us to over or underestimate the impact of things like scaling up R&D investments.

To make progress, we need experiments

Most of the approaches at trying to get a handle on the software intelligence explosion so far have been either through theoretical modelling, conceptual arguments, or doing statistics on messy real-world data. In part, this is because few people have been thinking about the software intelligence explosion in rigorous terms. And of the people that have, these approaches better fit their skillset, or are cheaper for them to implement.

But we think we’ve squeezed out much of the value from these approaches given existing data, and on the margin there’s a better approach — experiments. This helps us get much higher quality data that more directly tests the hypothesis and removes confounding factors. It also lets us test whether key assumptions will hold to help inform how we think about the software intelligence explosion, like in terms of models.

Here are some examples that we think are especially important:

Studying how much software progress is due to data. If we learn that most software improvement comes from increases in data quality, that could reduce our credences in the chances of a software intelligence explosion.¹² However, existing approaches are based on high-level statistical analyses of actual papers, where we can’t control which algorithms or training data are used. So it’s hard to say which innovations are most important, or how important data is. In contrast, experiments would offer a much higher degree of control.

Understanding how much compute is a bottleneck to software progress. In the software intelligence explosion, we can get lots of software progress even if we don’t use a lot more compute. So we want to know how hard it is to find new algorithms that push the state of the art, even without using much compute to run experiments. However, there isn’t much real-world data that tells us how easy this is. So we want to run experiments to see whether this is possible — this might mean randomly allocating compute budgets to different researchers to see how that impacts the amount of software innovation they’re able to achieve. We might also want to perform scaling experiments to understand how well algorithms that work with small training runs to large ones — if this happens easily, compute might not be as big of a bottleneck as we think.

Importantly, just doing experiments isn’t going to be a silver bullet. We might still work with flawed models. Experiments might also be impractical — for example, if we want to test how well software innovations apply at frontier training scales, we need enough compute to do a frontier training run! That restricts the number of actors that can study this kind of question dramatically. So we’re skeptical that this will “solve” questions about the software intelligence explosion.

And there’s still some role for other approaches. For example, we might want to know which input most bottlenecks software progress — is it intelligence, compute, engineers, or something else? Besides experimental approaches, we could try and see if software progress mostly comes from large labs that are compute rich, or from the same set of researchers over and over.

But on the margin, we think experiments are the most promising avenue for improving our understanding about the software singularity. And if the software intelligence explosion is actually real, it might be especially important to gather evidence on these questions as soon as possible.

We’d like to thank Greg Burnham, JS Denain, Jaime Sevilla, Lynette Bye and Phil Trammell for feedback on this post.

Technical appendix

In the main post we elided over many of the technical details to make our results widely accessible. But if you’re one of the more technically-minded readers of our newsletter, you’ll also be interested in our modeling and data choices, so we specify these here.

Estimating the returns to R&D using the Jones model

Let $A$ denote some measure of software quality, which is improved via a Jones-style idea production function:
\[\frac{dA}{dt} = A^{1-\beta} F(L,K)^\lambda; \beta, \lambda > 0\] $A^{1-\beta}$ represents ideas possibly getting harder to find over time, while $F(L,K)$ denotes the effective research input given experimental compute $K$ and cognitive labor $L$. Suppose research is automated in such a way that $F(L,K)$ shifts to be proportional to the effective number of simulated AI researchers, which is given by $Ac$ for some constant $c$.¹³
\[\frac{dA}{dt} \propto A^{\lambda + 1 - \beta} c\]
This model says software progress growth is hyperbolic if $\frac{\lambda}{\beta} > 1$. In the terminology of the post, $r = \frac{\lambda}{\beta}$ is the “returns to AI research.” Therefore, we have a software-only intelligence explosion if the returns to AI software research are sufficiently high.

In the following section, we describe how we estimate the returns to AI research for frontier language models. The key to measuring this is getting some input measure of $F(L,K)$.

Approach 1: The number of papers

One approach is to proxy for $F(L,K)$ based on the number of papers that are produced.¹⁴ This is the same approach as used in previous work.

We do this in domains of AI for which we have estimates of the relevant rates of software progress — namely computer vision, reinforcement learning, and language modeling. We use these estimates to define the “software quality”,¹⁵ which we use as our output metric.¹⁶

We get data on the number of papers in different years from OpenAlex, which we identify using the following “concept” codes:

Computer vision: Computer vision (C31972630) and Deep learning (C108583219)
Reinforcement learning: Reinforcement learning (C97541855)
Language models: Natural language processing (C204321447) and Deep learning (C108583219)

The resulting estimates of the parameters are shown in the table below:

	Computer vision	Reinforcement learning (Atari)	Natural language processing
$$\lambda$$	1.038 (0.245 to 4.259)	1.165 (0.250 to 4.362)	0.835 (0.187 to 3.637)
$$\beta$$	1.302 (0.269 to 5.571)	1.299 (0.241 to 5.581)	1.586 (0.322 to 7.148)
$$r$$	1.262 (0.727 to 2.094)	1.201 (0.380 to 2.708)	1.892 (1.069 to 3.212)

Estimates of key parameters in the Jones model, proxying R&D inputs with the number of papers in certain domains. We provide median estimates, and show 90% credible intervals in brackets. Code for this analysis can be found in this github repository.

We then estimate the returns to R&D using Bayesian inference.¹⁷ Like in computer vision and reinforcement learning, this yields central estimates of $r$ that exceed 1, and in fact the central estimate is higher in language models. Moreover, the 90% credible interval exceeds one as well — pointing towards a software intelligence explosion! On the other hand, all of these estimates have very large uncertainties, so the confidence intervals across these different domains overlap quite a lot.

Proxy 2: Some function of cognitive labor and experimental compute

In reality, we might think that papers are a poor proxy for R&D inputs. For example, AI R&D involves lots of people training models, but the “number of published papers” doesn’t directly model these people at all.

So we consider an alternative approach that treats the R&D input as some function of training compute and AI researcher labor at OpenAI from 2022-2025.

The next approach will try to directly measure $F(L,K)$ instead of proxying it. Suppose that software progress is growing at a constant rate, which is consistent with the empirical evidence we have so far (see here, and here). That implies the Jones equation is at a steady state, i.e.,
\[ g_A = \frac{\lambda}{\beta} [\epsilon_K g_K + (1 - \epsilon_K) g_L] \] In this equation, $g_A$, $g_K$, and $g_L$ denote the growth rates of $A$, $K$, and $L$ respectively. $\epsilon_K$ denotes the elasticity of $F$ with respect to $K$ — so if you increase $K$ by 1%, $F$ increases by $\epsilon_K$ percent. Re-arranging this equation results in the following:

\[\frac{\lambda}{\beta} = \frac{g_A}{\epsilon_K g_K + (1-\epsilon_K) g_L}\]

Intuitively, this equation says that $\frac{\lambda}{\beta}$ is equal to the ratio of research output divided by research inputs. We can now estimate the terms on the right-hand side by considering frontier AI labs after November 2022, when ChatGPT was first released. Note that we give growth rates in base $e$.

$g_K \approx 1.3$ from data on OpenAI’s annual compute spend
$gL \approx 0.85$ from data on OpenAI’s staff counts over time
$\epsilon_K \approx 0.67$ based on the fact that if markets are competitive, the elasticity of output with respect to capital should equal the compute share, the share of research money spent on compute instead of researchers. We guess the compute share is about 0.59 to 0.75.¹⁸ As a central estimate, we take the average of 0.67.¹⁹
$g_A \approx 1.1$ based on estimates of training compute efficiency improvements in language models.

The nice thing about this approach is that it doesn’t rely on the weak proxy of the “number of papers”. But it instead requires making an additional assumption, which is that software efficiency has grown at a constant rate.

Compute bottlenecks

One issue with the Jones model, pointed out in Whitfill and Wu 2025 and in Erdil and Barnett 2025, is that there may be compute bottlenecks.

Rigorously, if $F(L,K)$ is a production function such that both inputs are necessary for sustained growth, then even if $L$ is increasing due to more simulated AIs, if experimental compute $K$ is not growing quickly, then $F(L,K)$ becomes proportional to experimental compute, not proportional to the number of simulated AIs, which breaks the argument for an intelligence explosion no matter what value $\frac{\lambda}{\beta}$ is.

One baseline case to consider is a Cobb-Douglas baseline:
\[ F(L,K) = L^{1 - \epsilon_K} K^{\epsilon_K} \] Here, the lack of $K$ doesn’t fully bottleneck progress as you can always still increase $L$ to get more output, but there is some penalty for increasing only $L$ instead of both $L$ and $K$. Under this assumption, the key intelligence explosion parameter becomes $(1 - \epsilon_K) \frac{\lambda}{\beta}$.

Given our estimate that $\epsilon_K \approx \frac{2}{3}$, that means all our estimates of $\frac{\lambda}{\beta}$ should be cut by a factor of three, which puts them all below 1.

Parallelizability in the Jones model

To address the issue of parallelizability in the Jones model, Phil Trammell proposes an alternative model where the impact of R&D inputs is mediated by the current level of software quality. This is shown in the equation below, where $A$ is software quality and $R$ is research input:

Here the CES function between $A$ and $R$ on the right-hand side prevents you from just being able to immediately increase $A$ by a ton just by increasing $R$ by a ton, because $\rho < 0$. But while this deals with the parallelizability issue, it unfortunately also makes things harder to estimate!

Notes

This is sometimes called the “software-only singularity”. ↩
We describe the full model in the technical appendix. ↩
Things may be more complicated in the short-run — this parameter primarily determines the long-run asymptotic dynamics of AI R&D, rather than the short-run. ↩
If $r < 1$, this feedback loop fizzles out. If $r = 1$, we’re in the special case where growth in inputs results in proportional growth in outputs – but that also means that we don’t get a massive “intelligence explosion”. ↩
This doesn’t mean that AIs only improve AIs when there’s a software intelligence explosion. This happens regardless — the question is whether these improvements happen fast enough to lead to an “explosion”, as opposed to “fizzling out”. ↩
Technical details on data and the model are provided in the technical appendix. ↩
One counterargument is that it’s possible that algorithmic innovations proposed outside of major AI companies tend to be much less useful, because it’s not clear that they’ll work at the compute scale of frontier AI models. ↩
To get a sense of the numbers, we know that OpenAI has more than doubled their compute stock in the last year, and AI companies are almost doubling their staff headcounts each year. Relatedly, we also know that private sector companies own an increasing share of GPU clusters, and the academic share of notable machine learning models has decreased over time. So if we look at the aggregate of OpenAI and academia, we’d measure slower growth in both labor and compute, and thus overall R&D inputs. ↩
Moreover, the input and output metrics are themselves often extremely uncertain. For instance, existing estimates of software progress are themselves based on observational estimates. Prior estimates of the returns to R&D are also unrealistic — for example, the exponent on research inputs in the Jones law of motion is greater than 1, so doubling researchers could more than double software efficiency! Part of the issue here is that these individual exponents cannot be estimated well due to data constraints, but the hope is that the overall returns can still be estimated reasonably well. ↩
In particular, Whitfill and Wu 2025 estimate whether compute and labor are complements or substitutes. If you don’t account for the dynamic where frontier scale is necessary, you find that compute and labor are substitutes. But if you do account for this you find that they’re very strong complements! ↩
Yet another issue is that there’s no explicit data in the model proxying for research inputs based on compute and labor. In practice, developing better capabilities also depends on data. ↩
On the other hand, AI systems could improve data quality through things like verification and filtering, generating more diverse problems, or helping build high-quality RL environments. So even if most software improvements boil down to data quality, we could conceivably see a software intelligence explosion. ↩
If $A$ is inference compute efficiency, then this equation holds exactly. If $A$ is training compute efficiency, then this equation only holds if the effective number of AI researchers (because they are getting smarter) is linear in training compute. ↩
This data is taken from OpenAlex, based on papers grouped into both “Natural Language Processing” and “Deep learning”. ↩
Software quality is tricky to define, but can be defined with reference to algorithms of previous years. For example, suppose we choose 2024 as our start year, where software quality is defined as 1. Compared to models in 2024, models in 2025 might need around three times less training compute to achieve the same performance. So we then say that algorithms in 2025 have three times higher software quality than algorithms in 2024. Note that this dubiously assumes that all software (algorithms and data) in a particular year have the same quality. ↩
Strictly speaking, these works provide a single growth rate of the R&D output metric, rather than the output metric itself. Other domains like computer chess have much higher quality R&D output data, since we can look at chess engine ELO scores. This gives a time series rather than a single average trend. ↩
This approach is detailed in Erdil, Besiroglu and Ho 2024. Based on the paper, we select relatively uninformative priors to avoid biasing results, where exponential growth is the typical outcome. We need to use this approach rather than things like maximum likelihood estimation because we only have a single trend over time, rather than an actual time series. ↩
We take this estimate from OpenAI’s 2024 budget, which shows 700 million spent on salaries and 1 billion on research compute, giving a naïve capital share of 59%. If we do a more sophisticated analysis that adjusts for spend on research staff only, include equity and a broader set of R&D, then we get about 75%. ↩
Note this term is not necessarily constant over time, so consider it a single snapshot. ↩

About the authors

Anson Ho is a researcher at Epoch AI. He is interested in helping develop a more rigorous understanding of future developments in AI and its societal impacts.

Guest author

Parker Whitfill is a PhD candidate at MIT in Economics. He is interested in understanding AI progress and its implications for the economy.