The best we have seen a model perform on a single run of FrontierMath is 29%.¹ If you want to use a model to solve FrontierMath-style problems, that’s the number to consider.

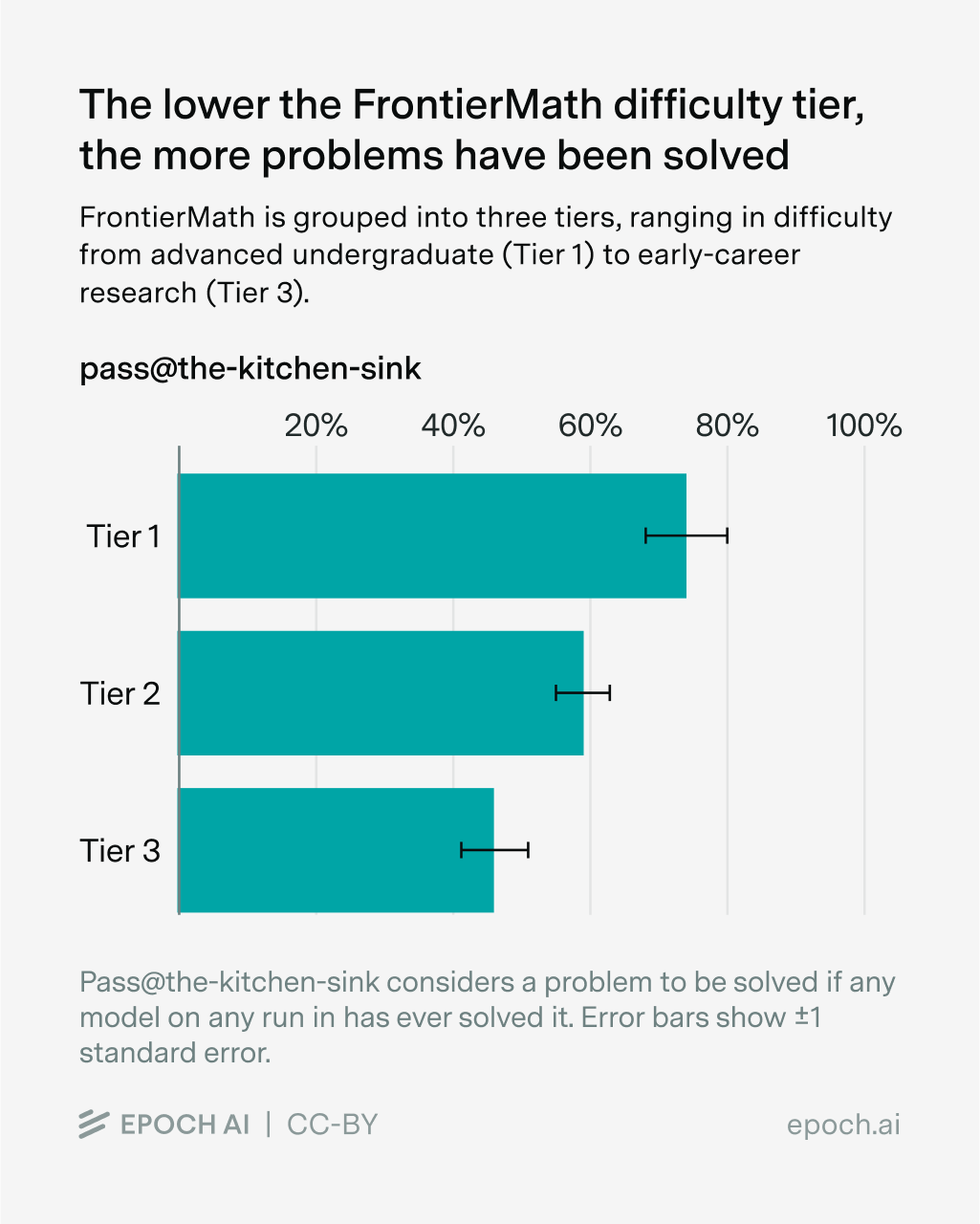
But there’s another way to gauge state-of-the-art performance: how many FrontierMath problems have been solved by any model, on any run, even once? This tells us more about what is “within reach” for today’s models. It’s also more forward-looking: if today’s models can generate the right ideas to solve a problem at all, then that makes it more likely that tomorrow’s models will be able to solve the problem reliably.² In other words, we can get a view of the future that’s a bit more concrete than just extrapolating accuracy trends.

To make matters more interesting, there’s some empirical evidence that if you run an LLM on a benchmark N times, the percentage of problems correctly solved at least once (known as pass@N) increases proportionally to log(N). If that’s true in general, then, since log(N) is unbounded, we should expect pass@N to approach 100% as the models are given more tries. Could FrontierMath’s saturation already be so clearly within sight?

To investigate this, I conducted 32 runs of GPT-5 (high).³ In short: FrontierMath isn’t dead yet. Pass@N on these runs show sub-logarithmic growth and appears to cap out below 50%.

That’s just one model, though: we have a bunch of other model runs sitting around that seem just as relevant for understanding what’s likely to be reliably solvable soon. Throwing them all together gives a pass@the-kitchen-sink of 57% — that is, how many problems were solved by any model on any run. Moving into guesswork territory, we estimate that even repeatedly running all of these models would cap out below 70%.

Going forward, it will be interesting to see how much progress on FrontierMath accuracy comes from shoring up reliability on this 57% of problems vs. solving problems models haven’t solved before.

GPT-5’s pass@N caps out below 50%

The chart below shows pass@N across our 32 runs of GPT-5 on our scaffold. Note how the pass@N curve is concave down compared to the straight line of a logarithmic fit.

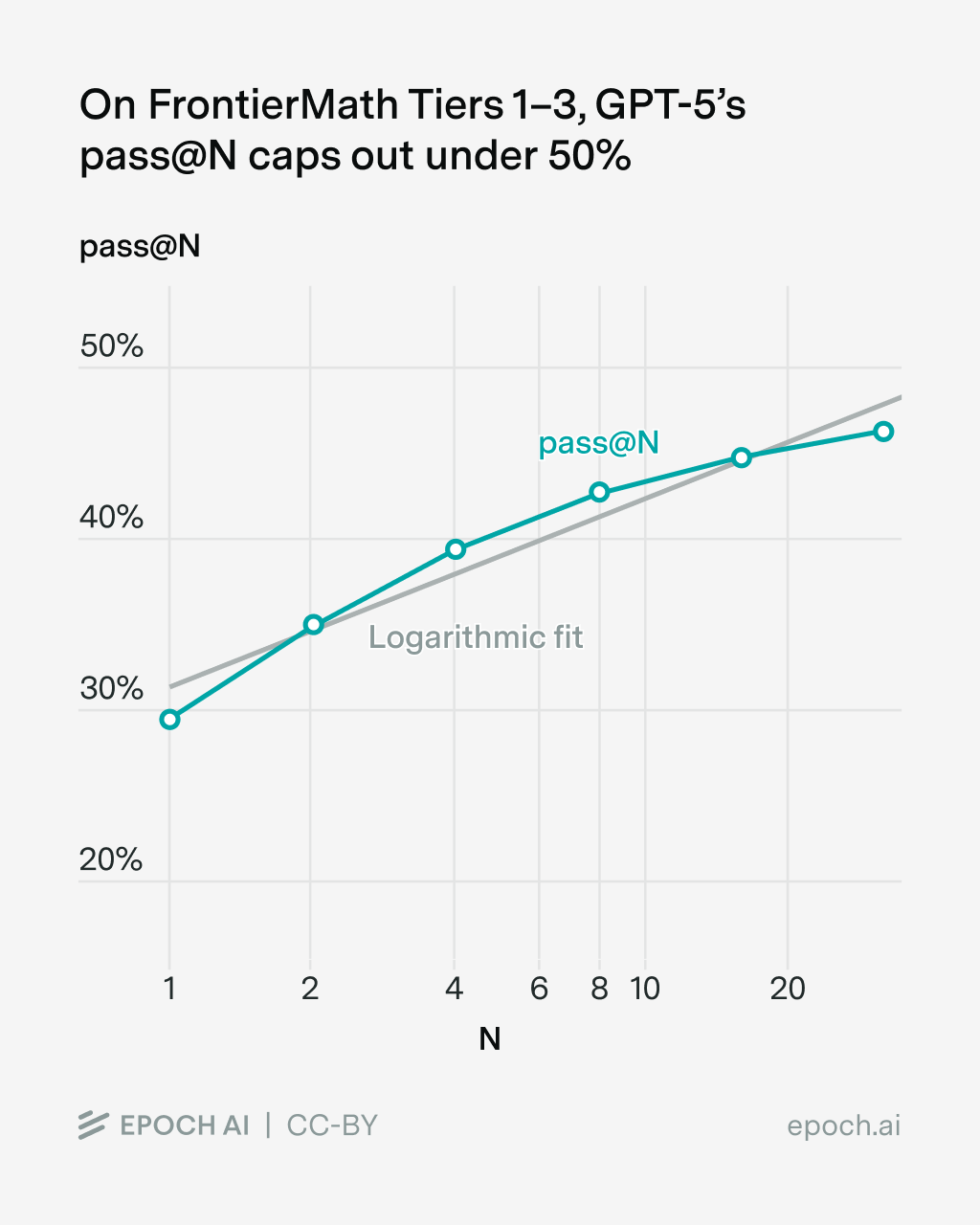
Below is the same data in a table. Each doubling of N increases pass@N, but by a smaller amount than the previous doubling. At the extremes, doubling N from one to two increases pass@N by 5.4%, but doubling N from sixteen to thirty-two increases pass@N by only 1.5%.

GPT-5 Pass@N on FrontierMath Tiers 1–3
N	Pass@N	Gain from 2x	Diff in Gain	# Solved
1	29%	--	--	85
2	35%	5.4%	--	101
4	39%	4.5%	-0.9%	114
8	43%	3.3%	-1.2%	123
16	45%	2.1%	-1.1%	130
32	46%	1.5%	-0.6%	134

How much more would pass@N increase with additional doublings? On average, the gains from doubling decreased by about 1% with each doubling. If we extrapolate that, we would see a gain of 0.5% as N goes from thirty-two to sixty-four, and that would be it. Maybe there’s a bit of a longer tail, but as a rough round-number guess, it seems likely that pass@N here would cap out below 50%.⁴

To sanity check this, I randomly drew ten problems that were not solved in any of these runs, and sampled them each 100 more times, for 132 total i.e. about two more doublings. None of these problems were solved even once. This is consistent with the observed data: we wouldn’t expect a draw of ten problems to hit one of the few problems that may be within reach of two more doublings. But this at least rules out the possibility that there’s a gold mine of problems that GPT-5 can get right if only it’s given 100 more chances.⁵⁶

Pass@the-kitchen-sink likely caps out below 70%

What about models other than GPT-5, or scaffolds other than Epoch’s? It’s a bit messy, but we can at least look at the assortment of FrontierMath runs Epoch has accumulated over time. We call this pass@the-kitchen-sink, and at the moment our kitchen sink is filled from the following six buckets:

• 32 runs of GPT-5, described above
• 52 runs of various models from various developers from Epoch’s benchmarking hub
• 16 runs of ChatGPT Agent conducted by OpenAI and graded by Epoch
• 1 run of a Gemini 2.5 Deep Think, evaluated manually
• 20 runs of o4-mini conducted a few months ago as part of an open-ended exploration
• 6 miscellaneous runs conducted while experimenting with o4-mini, Gemini 2.5 Pro, and Grok 4

All together this gives a pass@the-kitchen-sink of 57%, or 165/290 problems solved.

Of these problems, 140 are solved in at least two buckets. This suggests that models do not have very different skill profiles, even ones from different developers: if one model can solve it, another probably can too. The table below shows how many problems are solved uniquely within a given bucket, as well as the bucket’s overall pass@N rate. Note in particular that our 32 runs of GPT-5 only solved a single problem that we hadn’t seen solved in some other run before!

Bucket	# of Problems Solved Only in This Bucket	Pass@N
ChatGPT Agent (N=16)	14	49%
GPT-5 (N=32)	1	46%
Epoch Hub Runs (N=52)	7	37%
o4-mini (N=20)	1	33%
Misc. Experiments (N=6)	0	33%
Gemini 2.5 Deep Think (N=1)	2	29%

The one notable deviation from this is ChatGPT Agent, which solved 14 problems (5%) that no other model solved. There’s a salient explanation for this: it’s the only model here with access to a web search tool. While FrontierMath doesn’t contain pure “look-up” problems, it does have some problems that are meant to be solved by appropriately adapting somewhat obscure knowledge, so we expect web search to help.⁷

Since we have 16 runs of ChatGPT Agent, we can look at how Pass@N scales as above. Doing this, we see a similar sub-logarithmic pattern: the returns to doubling N decrease by about 1% (absolute) with each doubling. Simple extrapolation suggests there might be another 6% to gain from additional doublings.

ChatGPT Agent Pass@N on FrontierMath Tiers 1–3
N	Pass@N	Gain from 2x	Diff in Gain	# Solved
1	27%	--	--	80
2	34%	6.9%	--	99
4	40%	5.9%	-0.9%	117
8	45%	4.8%	-1.2%	130
16	49%	4.0%	-0.8%	142

Where would pass@the-kitchen-sink cap out?

We have clean estimates for GPT-5 and ChatGPT Agent. Conservatively assuming the gains from additional runs of these would be disjoint, that would add 7% in the limit, for a running tally of 64% total.

We don’t have as good a way to predict what all the other models would add, if re-run repeatedly. We can at least note that, across all our existing runs for them, they solve 46% of problems, but only 13 problems (5%) that neither GPT-5 nor ChatGPT Agent solved. This suggests fairly low marginal diversity, though we can’t rule out that one of these models would break into new territory if re-run repeatedly.

For the sake of a bottom-line number, I’ll assume that this pool has as much juice left to squeeze as ChatGPT Agent, the larger of our previous two estimates. Again conservatively assuming that these gains would be disjoint, this gives an all-in cap of 70%.

In the original release of FrontierMath, we estimated that 7% of problems were erroneous, either due to fatal ambiguities in the problem statement or issues in the answer key or verification script. We collect errors as we find them and will update the benchmark periodically, so this number will decrease over time. Currently we are only aware of uncorrected errors in 2% of problems. Conservatively taking the error rate to be 10%, we are thus left with 20% of FrontierMath problems being likely out of reach for current models.

Returning to the 57% of solved problems, we observe the expected pattern across the FrontierMath difficulty tiers: lower tiers have higher solve rates.

This gives us something to watch as models improve on FrontierMath

Epoch recently published a report on how we expect AI to look in 2030, which included the following projection of FrontierMath performance.

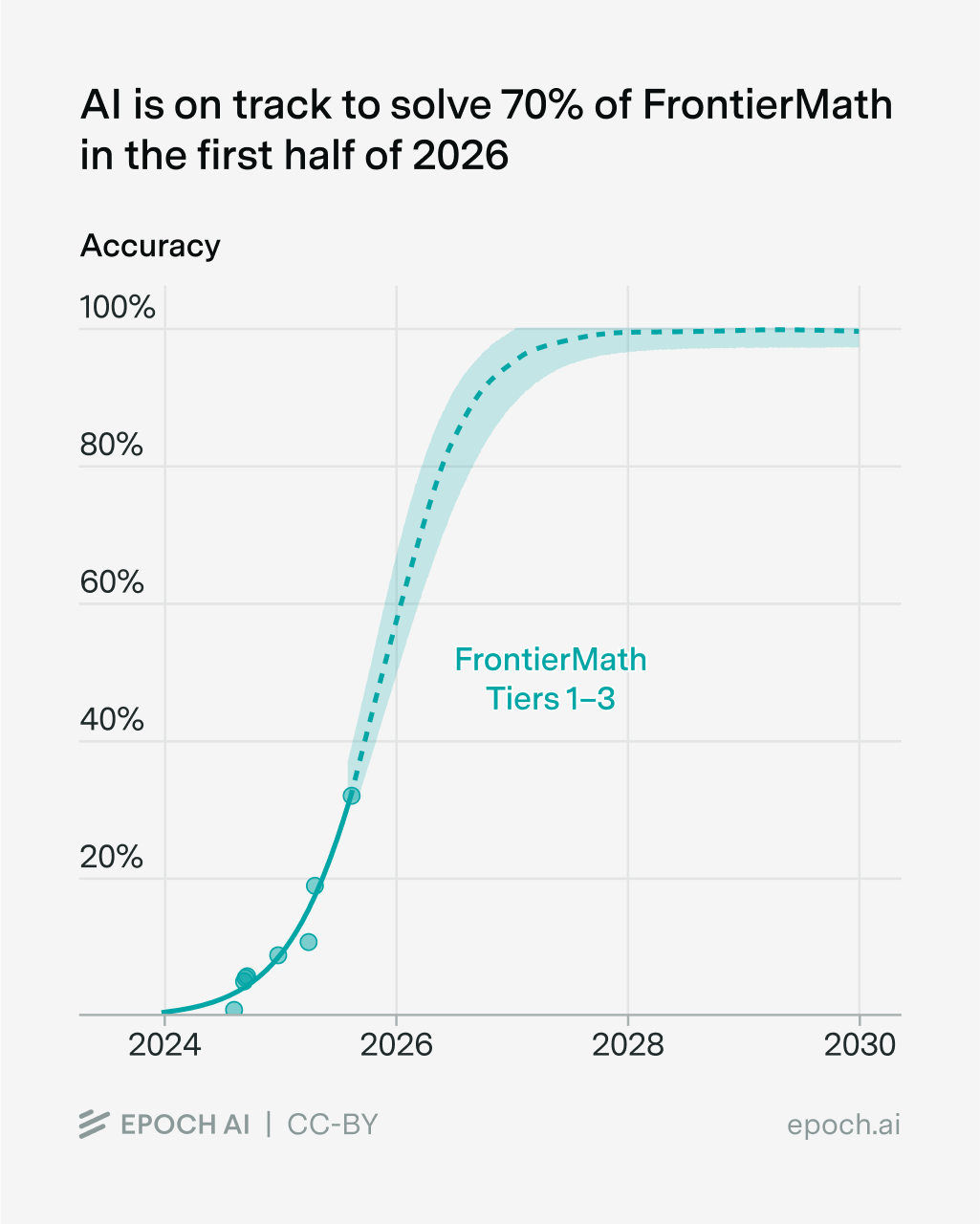
While a performance of 70% seems high compared to today’s SOTA, our projections show it arriving in the first half of next year. The investigations in this post make this seem believable: we have already observed some model solving almost that many problems. If additional training can simply shore up the performance observed in our pass@the-kitchen-sink, it will already be most of the way there.

By the same token, this gives us something more precise to look at if and when a model does hit this performance level. In particular, we can see how much of the gain comes from problems that we have already observed being solved at least once, vs. problems that haven’t been solved at all before.

In the extremes, the interpretation of progress is very different. If gains come entirely from previously solved problems, then this represents purely improved reliability. If, however, much of the gain comes from problems that no model has solved before, then we can interpret it as a meaningful advance in capability.

Thanks to OpenAI for API credits used for the GPT-5 experiments. Thanks to Daniel Litt for feedback on this post.

Stay one step ahead

Get the latest from Gradient Updates in your inbox

Subscribe

Notes

1. In this post, by FrontierMath, I always mean the private problems in Tiers 1–3. ↩

2. This reasoning is only valid for benchmarks where random guessing scores ≈0%, but FrontierMath is such a benchmark: answers are typically large integers or complicated symbolic real numbers, so we can sample repeatedly without worrying that models are getting correct answers just by luck. ↩

3. These runs were conducted with a 10x token budget compared to our usual scaffold. In the run currently shown on our benchmarking hub, GPT-5 scored 25% but exceeded our scaffold’s 100K token budget on 3% of problems. I tried giving it a 10x token budget, and it scored 29% while never exceeding the budget. For our experiments here, I used our standard scaffold with 10x the standard token budget. We’ll be increasing the general token budget in our scaffold going forward. ↩

4. That said, we can’t rule out that this is simply a very slow-growing function that is nonetheless unbounded, e.g. c*log(N) for small c, or log(log(N)). ↩

5. Of course, these experiments in general lack the power to tell the difference between p(solve)=0 and p(solve)=small. If we crudely model a problem as requiring k steps, and that GPT-5 has a probability of p of performing each step correctly, then p(solve)=p^k. For a problem with k=10 and p=½, GPT has a ≈50% chance of solving it in 709 samples. I would still want to count this problem as “within reach”. ↩

6. These problems were also chosen from among those that no other model run solved. These runs are discussed further on in the post. ↩

7. We plan to experiment with adding this. ↩