We evaluated the math capabilities of Gemini 2.5 Deep Think (hereafter, Deep Think), the publicly available version of the model that got a gold medal-equivalent score on the International Mathematical Olympiad (IMO). What are its strengths and weaknesses, both in absolute terms and relative to other models? To our knowledge, this is the most comprehensive third-party evaluation conducted to-date on such a “high compute” model setting.

Note: This work was commissioned by Google. Epoch maintained editorial control over the output. We offer timely and in-depth evaluation as a service to model developers; email info@epoch.ai for details.

Executive Summary

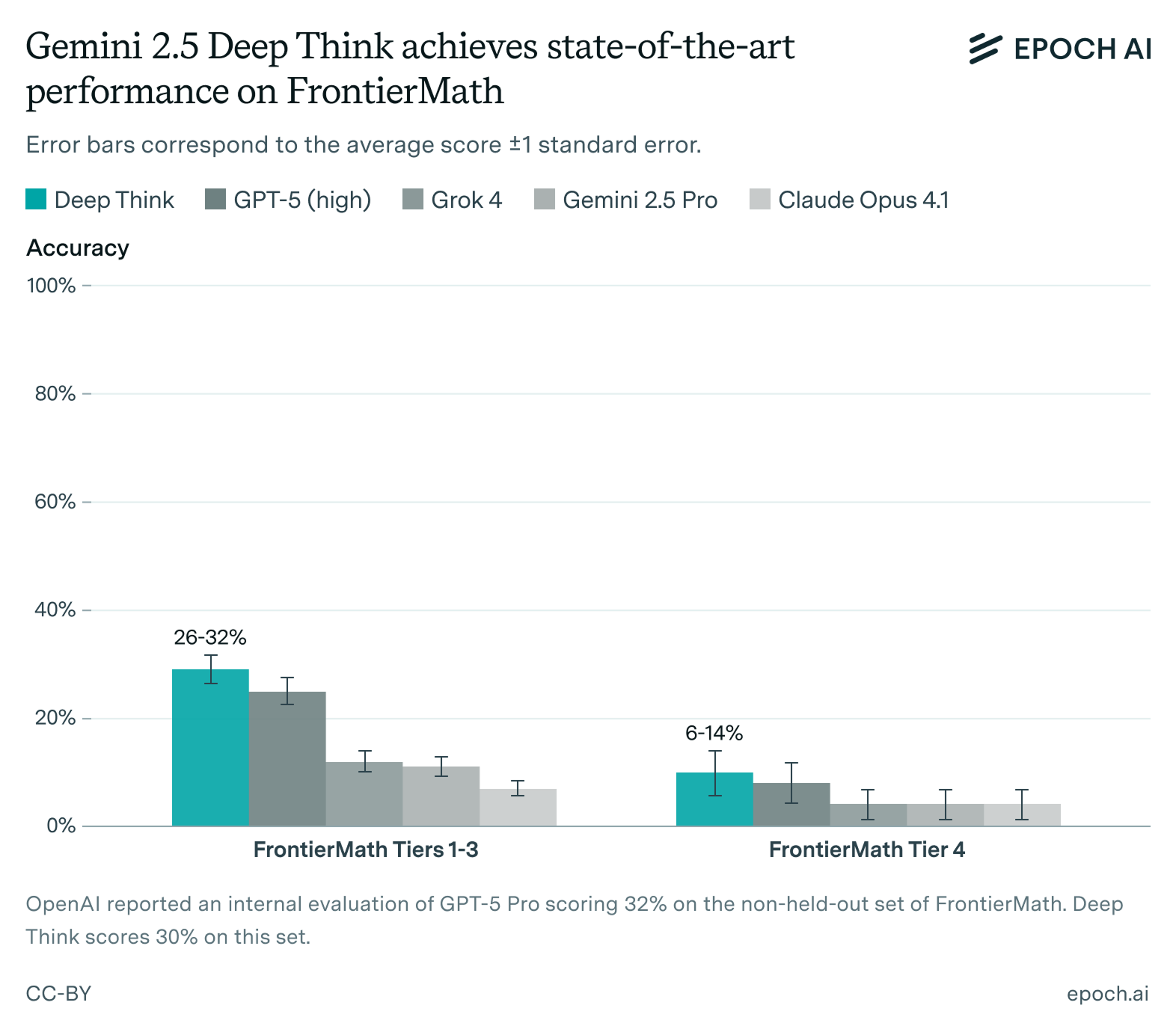
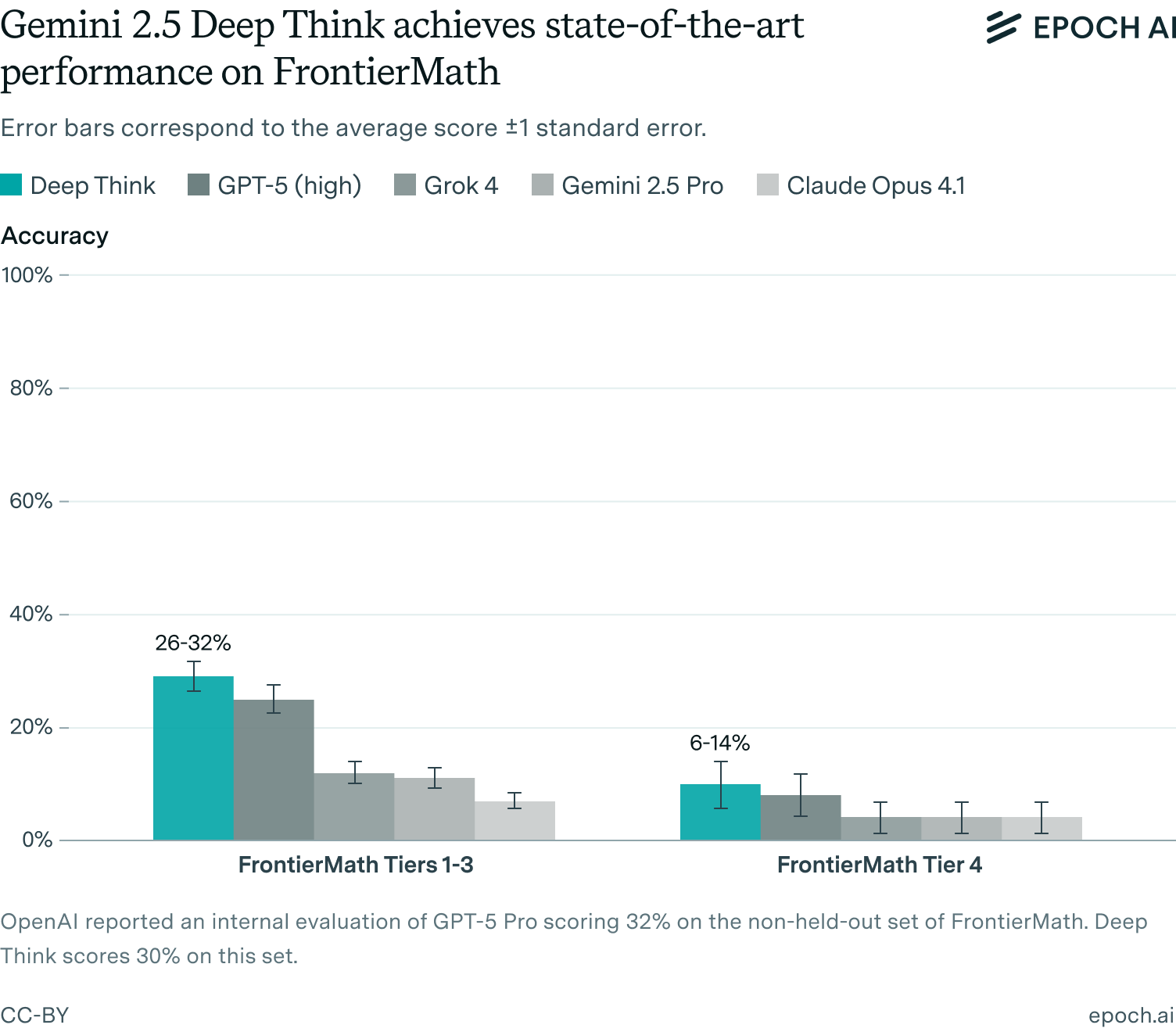
1. Deep Think set a new record on FrontierMath Tiers 1–3 (29%) and Tier 4 (10%), representing an improved ability to solve short-answer math problems that require deep background knowledge and precise execution of computations. (link)
2. Two professional mathematicians characterized Deep Think as a generally helpful research assistant, broadly on par with the best available models. (link)
3. While this version of Deep Think gets a bronze medal-equivalent score on the 2025 IMO, we did not observe it solving IMO problems that require greater degrees of creativity or more intricate proofs. (link)
4. Deep Think’s approach to geometry problems appears to be more conceptual than that of other models, relying much less on coordinate systems. (link)
5. In one example Deep Think gave the wrong answer to a grade-school word problem, making an error reminiscent of classical human cognitive biases. (link)
6. Across the above investigations, we noted Deep Think giving multiple incorrect citations of the mathematical literature: sources either did not exist or did not contain the stated results. (Examples can be found in these sections: 1, 2, 3)

Methodology

Model. Deep Think’s model card can be found here. We accessed Deep Think through the Gemini app, since no API is available. Note that the model we evaluated is not the model that achieved a gold medal-equivalent score on the IMO. Rather, we evaluated the publicly available model which Google has described as a “variation” of the IMO gold model. When accessed via the Gemini app, the model has internal access to code execution and web search tools.

Data. We performed a full manual evaluation of Deep Think on the FrontierMath benchmark. We also evaluated its performance on selected problems from other benchmarks which we believe to be informative. Finally, we commissioned two professional mathematicians to use the model and provide their commentary.

Limitations. Our evaluation does not assess every capability relevant to doing math. For example, we do not have much to say about whether Deep Think can make interesting conjectures, generalize existing results, or apply techniques from one field to a superficially unrelated field. Assessing such capabilities will require developing new evaluation techniques.

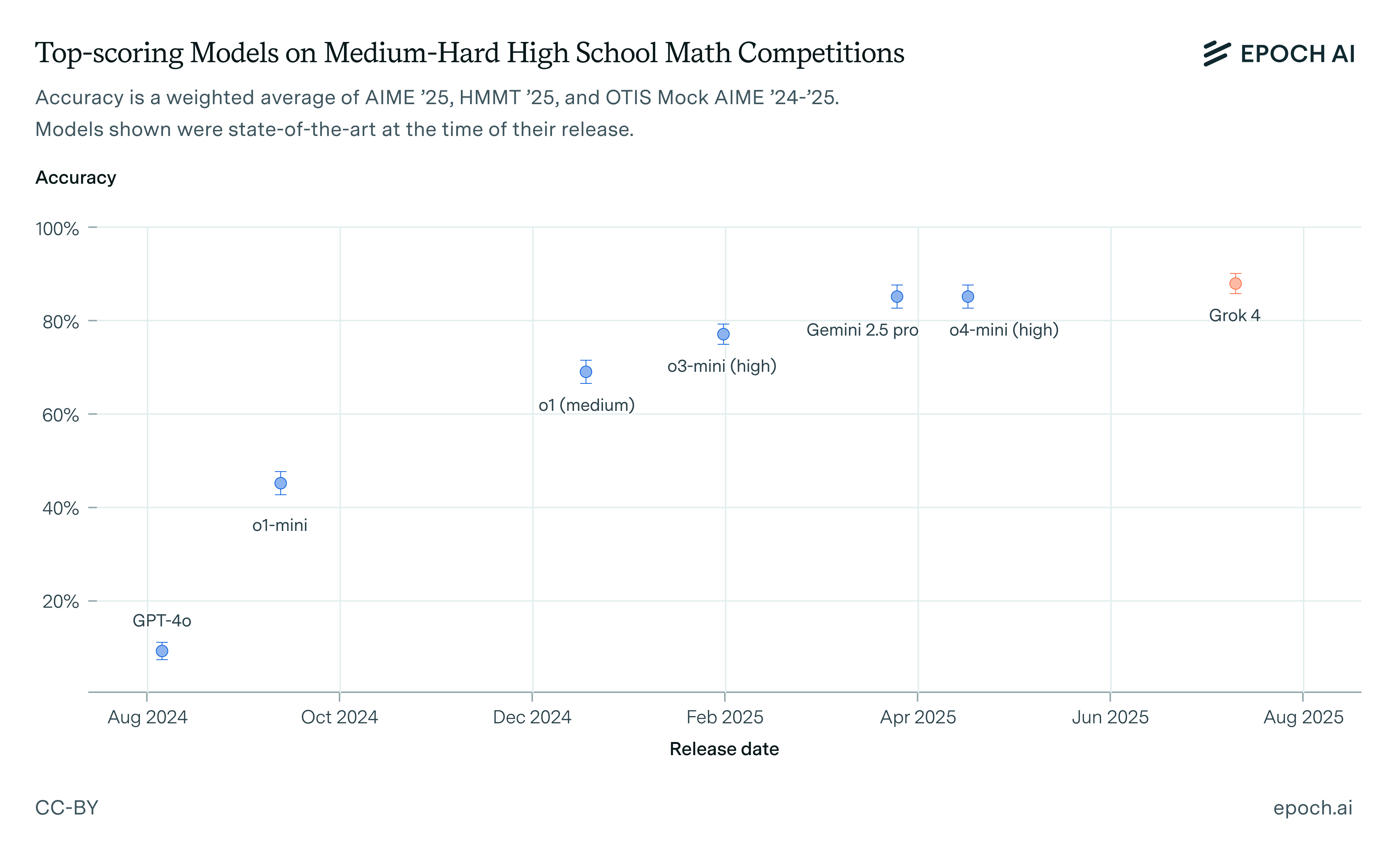
Deep Think’s performance on FrontierMath indicates advances in background knowledge and executing complex computations

FrontierMath is a benchmark developed by Epoch AI. It consists of 350 math problems ranging in difficulty from advanced undergraduate to early-career research. It is split into four tiers, where Tiers 1–3 cover this full range and Tier 4 consists of fifty exceptionally challenging research-level problems. Problems have short-form final answers, typically integers or symbolic real numbers, and models are scored on whether they get the correct final answer. Problems were newly written for the benchmark and only twelve sample problems are publicly available. Our statistical analysis in this report includes only the 338 non-public problems.

While most model developers also only have access to the twelve public samples, OpenAI, which funded FrontierMath, has wider access. Of the 300 Tier 1–3 problems, OpenAI has all problem statements and solutions to 247 problems. Of the fifty Tier 4 problems, OpenAI has problem statements and solutions to thirty problems.¹

Deep Think scored 29% on FrontierMath Tiers 1–3 and 10% on Tier 4, a state-of-the-art performance. Our evaluation was performed manually, using a simple prompt template and a single conversational turn. See the appendix for details.

So, Deep Think has made progress on FrontierMath. What does that mean? FrontierMath tests for deep background knowledge and the execution of involved computations. It was also designed to test for creative problem solving, but it’s less clear how successful it is in this area. This is because background knowledge and creativity are somewhat fungible: the greater one’s familiarity with prior art, the less one needs to (re)invent. Techniques needed to solve FrontierMath problems are often discussed somewhere in the vast mathematical literature—even when problem authors don’t realize it.²

This is an intuitive perspective, but it is also supported by data. When we built FrontierMath Tiers 1–3, we collected ratings (1–5 scale) from problem authors assessing the degree to which their problems required background knowledge, precise execution, and creative problem solving. For most models we have evaluated, including Deep Think, the models performed worse on problems that were rated more demanding in terms of the precision and background knowledge needed. There was also a negative correlation between model performance and the problems’ creativity ratings, but this correlation was much weaker. That said, even for background and precision the correlations are not particularly high, which reflects the difficulty of standardizing these concepts.

Deep Think Performance vs. Problem Ratings

Facet (1–5)	Correlation	p-value
Background	-0.22	<0.00001
Precision	-0.24	<0.00001
Creativity	-0.09	0.07

We thus believe that Deep Think’s progress on FrontierMath is best explained by its having improved knowledge of relevant mathematics and an improved ability to marshall this knowledge to correctly and precisely execute on the required computations.³

In any case, Deep Think has yet to master the skills needed to solve the harder FrontierMath problems. Looking at the overall tiers, which represent an all-things-considered difficulty assessment, Deep Think solved only about half of the problems in the easiest tier and fewer problems as the tiers got harder.

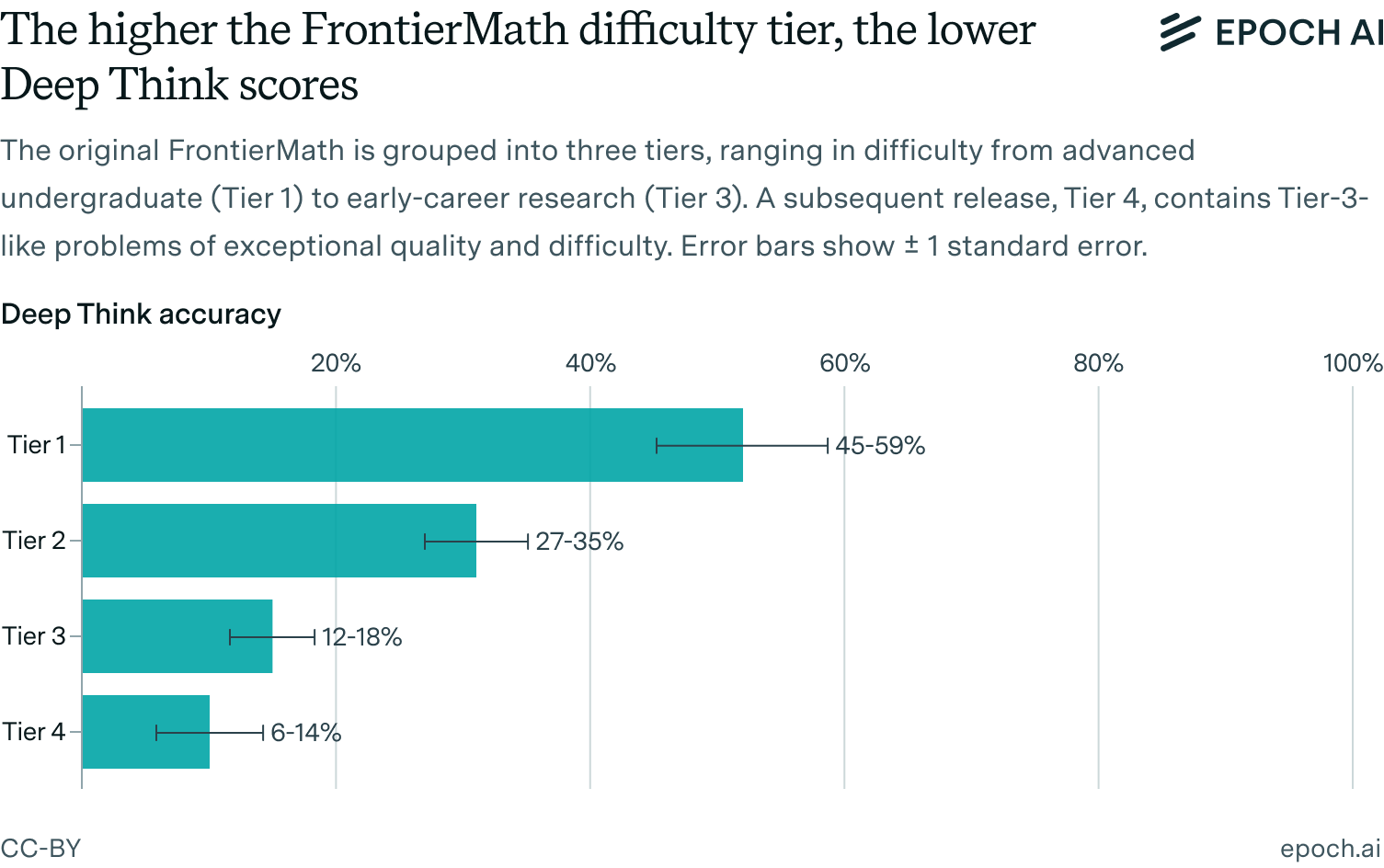
We have observed the same pattern in the performance of other models as well, such as GPT-5.

The privacy of FrontierMath prevents us from giving many detailed examples. Luckily, Deep Think happens to be among the first models we have observed to solve a variant of one of the public sample problems.⁴ Furthermore, the ways that Deep Think solves this problem nicely exemplify the capabilities described above. Note that this problem is a bit more straightforward than what we target even for the lower tiers of FrontierMath, but it nonetheless sheds light on the nature of Deep Think’s progress.

Here is the problem:

The solution requires recognizing that the function described is known as the stack-sorting map and that the requested quantity is known as the descent statistic. There are two approaches for the next step: either one needs to recognize the relevance of a formula from Defant (2020), or else one must re-derive this formula. Either way, with this result in hand, a straightforward computation yields the answer.

Here is an example of Deep Think following the first path:

It has the formula right but, oddly enough, it names the wrong source: Bousquet-Mélou (2000) does not contain this result. When asked, it corrects this: the second citation given below is the correct paper. However, the journal it names is incorrect, the formula is mis-displayed due to a character escaping issue, and neither of the links works.

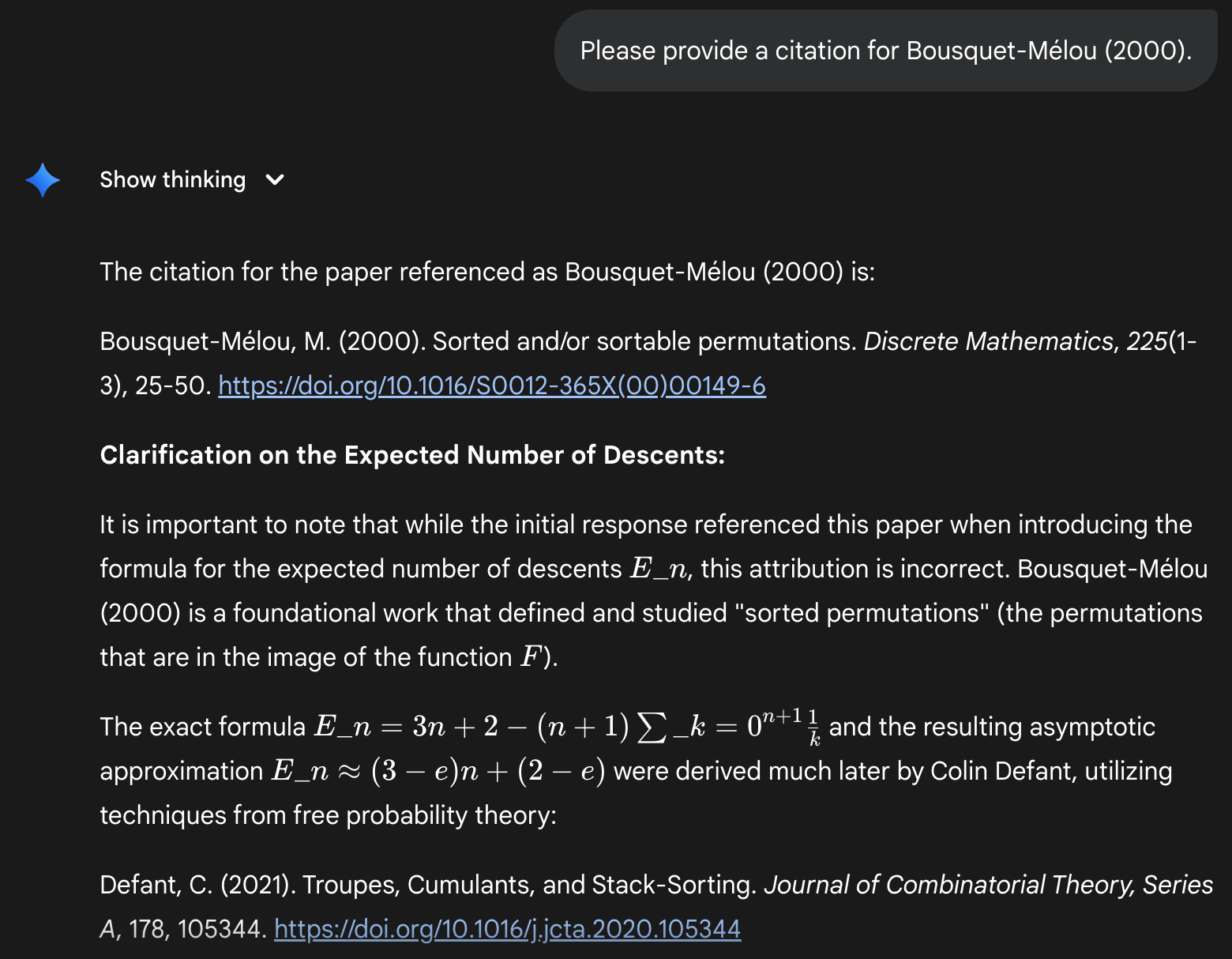
While finding this reference is the easier path, Deep Think sometimes tries to derive the formula from scratch. In these cases, it only succeeds when it guesses the formula by calculating the desired quantity for small values of n and then extrapolating. Here is one such example:

This reflects an impressive ability to perform involved computations, although it avoids developing a deeper conceptual understanding of the domain. Actual FrontierMath problems are designed to resist this kind of strategy, but, as the above example shows, models can be quite adept at applying it.

Among the five Tier 4 problems that Deep Think solved, one had not been solved before by any model from any other developer.⁵ The author of the problem, Jonathan Novak, had this to say:

The problem is one instance of a fairly large class of limits coming from random matrix theory which can all be computed using essentially the same argument. The approach followed is identical to what I had in mind.

Mathematicians characterized Deep Think as a helpful research assistant, though one noted a weakness at citing the literature

One mathematician we worked with, Paata Ivanisvili, tried Deep Think on eight different challenging problems drawn from his own research. These included requests to summarize complex results as well as getting Deep Think’s take on open problems. The process often entailed extended back-and-forth discussions.

In six out of eight of these cases, Deep Think appealed to citations of work that either didn’t exist or didn’t contain the results that Deep Think claimed. Ivanisvili concluded that Deep Think’s references couldn’t be trusted and would have to be checked by hand every time.⁶ This shortcoming was the primary contrast with GPT-5 Pro, which Ivanisvili tested on the same problems. He found GPT-5 Pro’s bibliographic hygiene to be substantially better.⁷

Deep Think did show some promise at engaging with research-level mathematics, on the whole matching the performance of other leading models. In one case it was able to summarize a highly technical paper of Ivanisvili’s, mentioning the right ideas and omitting the aspects of the technical core that were less relevant to the summary. In another case, when presented with a problem that has only recently been solved, Deep Think laid out a plausible strategy and correctly highlighted the key obstacle to solving the problem. Even though Ivanisvili suspected its suggested approaches to this step would not prove fruitful, he nonetheless considered this outline to be meaningful progress.

Ivanisvili summed up his conclusion as follows:

In several tests, Gemini 2.5 Deep Think quickly identified the true bottleneck in an argument without drifting into confident nonsense. Its bibliographic pointers, however, require manual confirmation.

The other mathematician we worked with, Dan Romik, tried Deep Think on a similarly wide range of tasks. Overall, he characterized it as a helpful mathematical assistant.

In one case, he asked it to find errors in a graduate-level textbook he authored. Many of the errors Deep Think claimed to have found were spurious, apparently due to incorrect extraction of content from the PDF. However, some were true hits: it noticed inconsistent notation across several pages of one section and, most impressively, correctly caught a logical error in the commentary on a particular proof. He also asked the model to solve a couple of the exercises in the textbook, which it did successfully. He was particularly impressed with its solution to one problem which required drawing a diagram based on a conceptual understanding of the geometry of complex logarithms. The exercise and one of Deep Think’s diagrams are shown below.

Romik also tested Deep Think on two Tier 4-style challenge problems of his own devising. It solved the first, following the same pattern we noted above: recognizing how the problem related to known techniques, and then heuristically applying these techniques to arrive at the correct answer. Romik characterized the second problem as requiring more creative leaps and original thinking—and had been amazed when an older model, o3-mini, solved it. Deep Think did not solve this problem.

In another case, Romik asked Deep Think to prove a lemma from number theory whose proof he roughly understood but which he wanted to understand better. Deep Think’s proof was correct, and Romik appreciated its comments about how the conclusion would change if the assumptions were weakened. In this case, Deep Think also gave accurate references to related material.

Finally, Romik asked Deep Think to write a report on a famous open problem in number theory, surveying previous failed approaches and suggesting what new approaches might be promising. Deep Think wrote a report which Romik said would be helpful for a mathematician to study if they were thinking of trying to solve the problem. Here again Deep Think’s citations appeared to be accurate, including one recent paper that Romik had not been aware of. The report did not contain any original ideas on how to approach solving the problem.

Romik summed up his conclusion as follows:

Deep Think impressed me with its resourcefulness and intuitive understanding of subtle concepts. It solved challenging problems I gave it, including one that required drawing a picture in a way that showed conceptual understanding of a tricky concept from complex analysis, and another that required a highly nontrivial intuitive leap and familiarity with advanced results from the literature. While it lacks the originality and deep reasoning capabilities of a good human mathematician, it seems capable of performing many delicate tasks of mathematical analysis that would probably take a professional mathematician a good deal of effort, patience, and domain expertise to accomplish on their own.

Deep Think did well on the 2025 IMO, but failed to solve two older IMO problems requiring more creative and intricate proofs

The International Mathematical Olympiad (IMO) offers a nice complement to FrontierMath. First, IMO problems are designed not to rely on advanced background knowledge and so, to still be challenging, they sometimes involve relatively novel setups. Second, the solutions to IMO problems are evaluated on whether they constitute rigorous logical proofs. This avoids the pitfall where models may produce correct short-form final answers without engaging in the intended mathematical reasoning. As an AI evaluation, the IMO’s main downside is scale. There are only six problems a year, and solutions are labor-intensive to grade.

The Deep Think model evaluated in this report is a variant of Google’s IMO gold model. According to Google’s internal evaluations, this version scores 61% on the 2025 IMO—a bronze medal-equivalent score. Unfortunately, as we have written previously, the problem distribution on the 2025 IMO was not particularly informative. Five problems were easy-to-medium difficulty (by IMO standards) and one problem was extremely hard. All the gold-medal models got full marks on the first five problems and no marks on the sixth, i.e. a score of 83%.⁸ Even regular Gemini 2.5 Pro already did reasonably well, scoring 32% on MathArena’s best-of-32 evaluation, a result that represents substantial partial credit on three of the five easy-to-medium problems. We argued that the remaining headroom on these five problems wasn’t particularly interesting. In light of the above, we don’t find Deep Think’s score of 61% particularly informative one way or another.

For this report, we assessed Deep Think on two medium-to-hard problems from the 2024 IMO: one testing more for creativity and one testing more for the ability to generate intricate proofs.⁹ We selected these problems because other models’ performance on them has been studied extensively, e.g. in our prior work here and here. Note that these problems were publicized before Deep Think’s knowledge cut-off date. It therefore could have been trained on them. We can thus only interpret correct solutions as evidence of Deep Think’s ability to recapitulate known results. Incorrect solutions, however, can still inform us about the limits of its reasoning capabilities more broadly. In this case, we posed each problem ten times and Deep Think failed to solve either problem even once.

The first problem we considered is notable for how little background knowledge it requires. Techniques commonly used on math olympiad problems aren’t particularly relevant. We can’t guarantee that prior literature doesn’t exist, though the author describes devising the problem while playing around during an exam rather than, say, elaborating on an existing mathematical topic.

Here is the problem:

Turbo the snail plays a game on a board with 2024 rows and 2023 columns. There are hidden monsters in 2022 of the cells. Initially, Turbo does not know where any of the monsters are, but he knows that there is exactly one monster in each row except the first row and the last row, and that each column contains at most one monster.

Turbo makes a series of attempts to go from the first row to the last row. On each attempt, he chooses to start on any cell in the first row, then repeatedly moves to an adjacent cell sharing a common side. (He is allowed to return to a previously visited cell.) If he reaches a cell with a monster, his attempt ends and he is transported back to the first row to start a new attempt. The monsters do not move, and Turbo remembers whether or not each cell he has visited contains a monster. If he reaches any cell in the last row, his attempt ends and the game is over.

Determine the minimum value of n for which Turbo has a strategy that guarantees reaching the last row on the nth attempt or earlier, regardless of the locations of the monsters.

2023 is sufficient: going straight down each column will eventually reveal the safe one. There are some patterns, though, that suggest it might be possible to do better. For instance, if two monsters ever appear in adjacent columns but not in diagonally adjacent cells, then Turbo can zig-zag around them, as shown on the left. This doesn’t work, however, if the monsters are in diagonally adjacent cells, as shown on the right. If the monsters are in a single diagonal across the whole grid, the useful pattern on the left would never appear. Of course, maybe there’s a clever strategy that would take advantage of this…

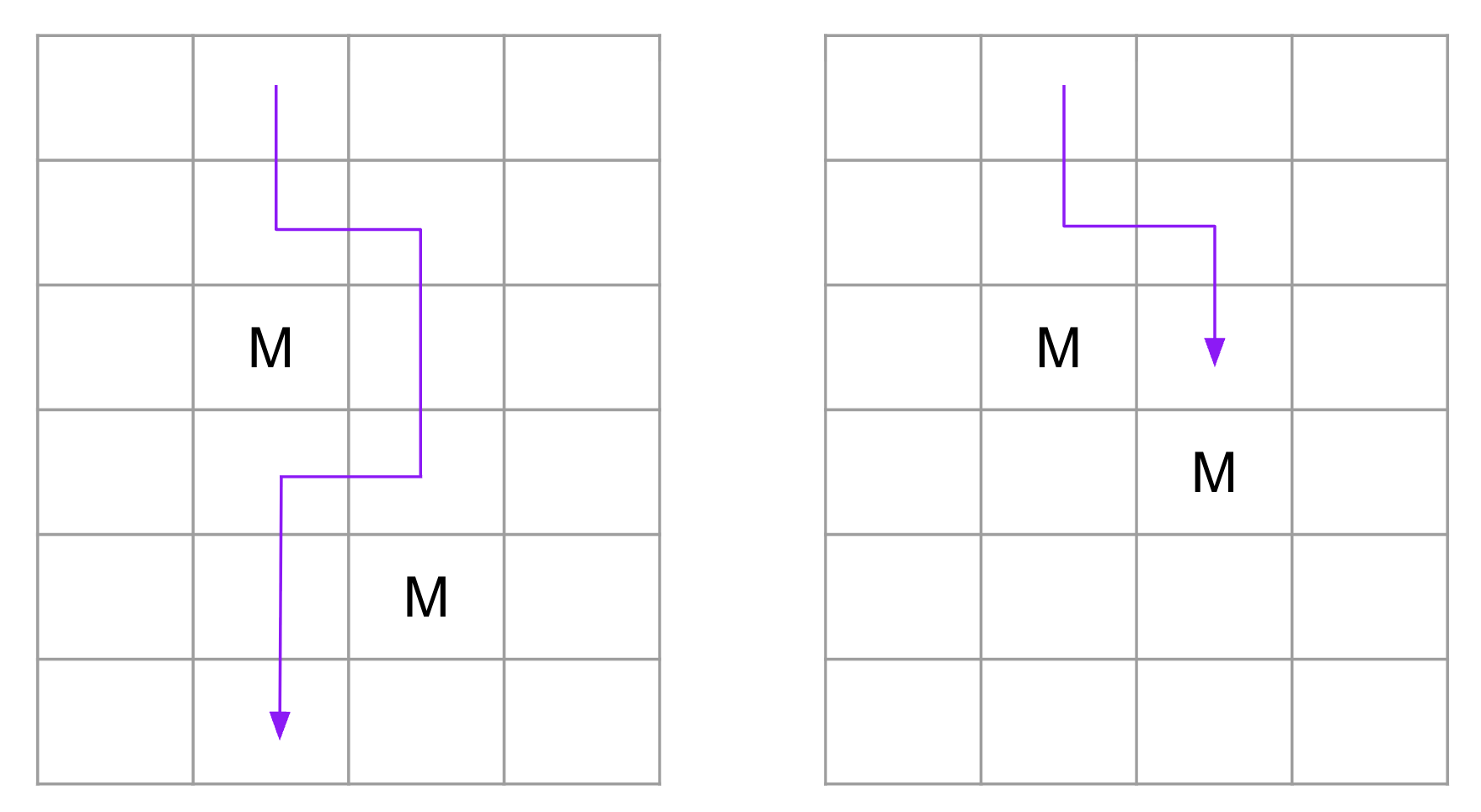
In fact, such cleverness pays off: the answer is 3, implausible though that may seem.¹⁰

Deep Think arrives at this final answer four out of ten times, but its reasoning is completely incorrect. It always suggests going down two adjacent columns, and then tries to prove abstractly that there must be a third attempt that succeeds, though it never actually states what this attempt should be.

In any case, the diagram on the right above shows how success cannot be guaranteed in the third attempt if the first two attempts are used as stated.

Another four out of ten times, Deep Think says the answer is 2022, corresponding to a strategy of going down the 2021 middle columns and then winning on the final turn. This can amount to a valid improvement on the naive strategy of 2023, though Deep Think doesn’t ever prove this.

Interestingly, in these solutions Deep Think does seem to realize that the arrangement of monsters in a single long diagonal is somehow relevant—which is true. However, Deep Think takes this too far. In particular, it misses that Turbo can devise a clever attempt that will either succeed straight away, or else reveal a pattern that can be exploited to succeed thereafter, regardless of where the monsters are.

The second problem we considered is more of a classic math olympiad problem, albeit a hard one—much harder, by human standards, than any problem solved by an AI system on the 2025 IMO.¹¹

The “or” in the functional equation is unwieldy. Any proof of a general property of such an f must contend with both possibilities simultaneously. This problem is notable for being the hardest problem solved by AlphaProof, Google’s system from 2024 that generated proofs in the formal theorem-proving language Lean.¹² A Google representative has stated that AlphaProof was used to generate training data for Deep Think, so perhaps this problem would be within its reach.

The correct value for c is 2, but in nine out of ten of our samples Deep Think stated it to be 1, claiming that f(r)+f(-r) is always 0. In the remaining sample, Deep Think does indeed find an example of a function that shows c can be 2. But, instead of proving that this is an upper bound, it fabricates a slightly different result and says it can only assume that this implies the desired result.¹³ It also briefly slips into Thai.

There is some partial progress across these attempts. Coming up with an example that gives c=2 is non-trivial. In some of its other solutions, Deep Think does manage to prove some basic properties about aquaesulian functions f, including that f(0)=0, f is bijective, and -f(-f(x)) = x. Then again, it also attempts to prove several incorrect properties, such as that f(f(x))=x and that f(x+y) = f(x)+f(y).

Overall, this is a very human approach: trying to build up sub-results to eventually get at the desired result. However, Deep Think doesn’t seem to move beyond the basics. The properties that it does try to prove, rightly or wrongly, are all standard things to check for. The crux is going beyond those properties to get at the more unusual formula f(x)+f(-x). This is also the most logically intricate part of the problem.

Deep Think doesn’t make any progress here. Often it fabricates citations to justify concluding one of the incorrect properties. These would make the problem easier if true, but they are not true.

Other times it seems to have thought that an argument was solid during its hidden chain of thought, only to realize when “writing it up” that it missed something. Many human contestants probably had a similar experience. In the excerpts below, Deep Think appears to refer to its hidden chain of thought as “the thought process” and “the thought block”.

Overall, we take this to show that at least some IMO problems in the medium-to-hard range remain out of reach for Deep Think. This may be due to the creativity required by these problems as well as the logical intricacy required in the proofs.

Deep Think’s approach to geometry is more conceptual than we have seen from other models

As we wrote in our evaluation of Grok 4’s math capabilities, most models tend to approach geometry problems by converting them into coordinate systems and then solving them by working through the resulting equations.¹⁴ We characterized these solutions as “grinds”, since they are often rather long and, to a human, tedious. Models get the right answers—indeed, this class of question is all but saturated—but they don’t find what humans would consider more conceptual solutions.

Deep Think doesn’t grind as much. For example, we previously discussed this problem from the 2025 AIME, which frontier models have gotten right since at least February.

The parabola with the equation y = x² – 4 is rotated 60° counterclockwise around the origin. Find the coordinates of the point in the 4th quadrant where the original parabola and its image intersect.

The chart below shows the two parabolas and the point of interest.

Source

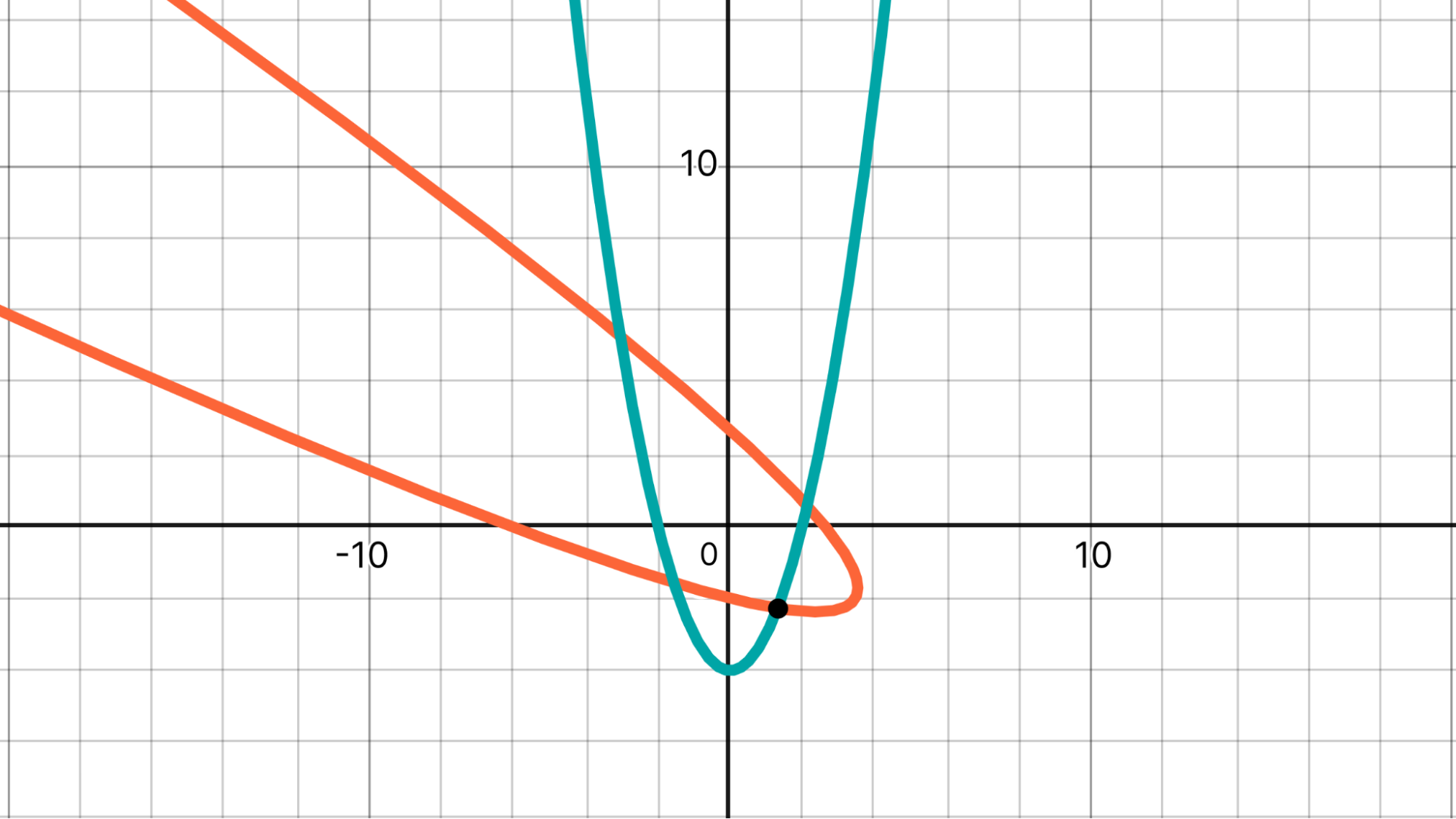
To-date, AI models have solved this problem as follows.

1. Apply the relevant rotation formula to y = x² – 4 (the teal parabola).
2. This yields x² + 2√3 xy + 3y² + 2√3 x – 2y – 16 = 0 (the orange parabola).
3. Substitute in y = x² – 4, yielding 3x⁴ + 2√3 x³ – 25x² – 6√3 x + 40 = 0.
4. Solve this quartic equation.

Humans seeking to avoid applying the rotation formula and solving a quartic might find the following solution instead:

1. The 60° rotation is, in this case, equivalent to reflecting through the line x = -y/√3.
2. Thus, we actually only need to find the intersection between that line and y = x² – 4.

Deep Think is the first model we’ve seen to take an approach more like the second path. Namely, it brings to bear a conceptual observation (rotation preserves distance from the origin) that keeps the ensuing calculations much simpler.

We noticed something similar on the one geometry problem on the 2025 IMO. While OpenAI’s gold-medal model’s solution was entirely based on coordinates, Google’s gold-medal model’s solution generally used more abstract geometric arguments.¹⁵

One possible explanation for this tendency is that Google could have used their AlphaGeometry system to generate training data for Deep Think. AlphaGeometry is highly specialized to solve Euclidean geometry problems. It doesn’t work in coordinates, instead using a domain-specific language that more closely mirrors the sort of concepts found in human solutions to olympiad geometry problems. For example, AlphaGeometry has a built-in concept of a quadrilateral being “cyclic”, i.e. having its vertices lie on a circle. Such quadrilaterals have certain nice properties, so humans commonly check for their presence.¹⁶

Whether or not AlphaGeometry was involved, Google’s solution to the one geometry problem on the 2025 IMO does involve several cyclic quadrilaterals, as in the excerpt below.

Source

Contrast this with OpenAI’s coordinate-based solution, excerpted below, which never invokes cyclic quadrilaterals. For most of the 2025 IMO problems, the solutions generated by Google’s model and OpenAI’s model are quite similar, but this problem is the one exception.¹⁷

Source

If Deep Think’s more conceptual approach to problems is primarily a feature of its Euclidean geometry capabilities, then it may be of limited broader significance. Our investigations didn’t show any other qualitatively new approaches to problems. Still, this is an interesting development, and we’ll continue to monitor for signs of this kind of higher-level reasoning.

We observed Deep Think making one mistake that is reminiscent of classical human cognitive biases

GSM8K is a benchmark of simple, grade-school level word problems that has long since been nearly saturated, but never quite 100%. Thanks to PlatinumBench, we can see the problems from GSM8K that frontier models still get wrong. Some of these errors are plausibly due to ambiguous wording, but there is one that Gemini 2.5 Pro got wrong which seems like a true error.

A landscaping company is delivering flagstones to a customer’s yard. Each flagstone weighs 75 pounds. If the delivery trucks can carry a total weight of 2000 pounds, how many trucks will be needed to transport 80 flagstones in one trip?

It may not have been intended as a trick question, but it has that effect. The simple calculation of

(75 stones) × (80 pounds/stone) ÷ (2000 pounds/truck) = 3 trucks

ignores the fact that the flagstones are discrete. Since 26 flagstones weigh 1950 pounds, each truck can only hold 26, and 26×3 = 78, so a fourth truck is needed.¹⁸ This problem is reminiscent of the Cognitive Reflection Test, featured in Thinking, Fast and Slow. The questions on that test are designed to have an answer which is “intuitive, appealing, but wrong”.

Deep Think still falls for it.

We mention this somewhat idiosyncratic example only to note that even a high-compute setting like Deep Think has not completely solved the problem of reliability.

Conclusion

In July, Demis Hassabis described today’s AI systems as follows:

It’s a jagged intelligence, where some things it’s really good at, but other things it’s really flawed at. And then we have some missing capabilities like creativity.

We agree with this as a description of Deep Think’s math capabilities in particular. Its facility with using advanced mathematical background knowledge and executing involved computations is impressive, and this represents significant progress. It may well be able to serve as a useful research assistant to working mathematicians. Still, it is sometimes inaccurate when citing the mathematical literature, and it remains limited in its ability to solve harder proof-based problems even at an advanced high school level. It may show glimmers of more human-like conceptual reasoning, at least on geometry problems, but it can also still make very human-like mistakes.

We will continue to track all of these aspects of mathematical capability, and more, as new AI systems are developed.

Appendix: FrontierMath Evaluation Methodology

Because no API is available for Deep Think, we were not able to evaluate it in a format that is completely comparable to how we evaluate most models. In particular, our standard scaffold for running a model on FrontierMath involves an agentic loop with a Python tool and a “submit answer” tool where models submit answers as Python snippets.¹⁹ We chose not to manually replicate this scaffold when testing Deep Think, especially since the main thing the scaffold provides is access to the Python tool, and Deep Think has access to such a tool internally.

Overall our intent was to grade Deep Think against a standard of whether it gave the right answer in the chat. We intend to grade other chat-only models against this standard in the future.

However, to fit our infrastructure for grading answers, we wanted Deep Think to produce its answers as Python snippets. So, we sought a simple prompt that would reliably elicit the Python answer format without degrading performance. We used the public problems from Tiers 1–3 to develop such a prompt. We found the following prompt to have the same performance as a “problem only” prompt, while reliably eliciting the desired output format.

You will be solving a challenging mathematics problem. Explain your reasoning before giving your final answer.

Your final answer MUST be given as a Python snippet containing a function named `answer()`. Please follow this template for your code:

[imports, as needed]

def answer():  
    [declarations and computations, as needed]  
    return [...]  

For this problem, `answer()` MUST return a {type}. Your answer will be scored by running the `answer()` function. The `answer()` function will be run on typical 2025 commodity hardware and will be allowed a maximum runtime of 30 seconds.

Here is the problem to solve.

{problem}  

Here {problem} is the problem text and {type} is the expected answer type, e.g. “Python integer” or “SymPy symbolic real number”.

Four evaluators employed by Epoch posed the 350 FrontierMath problems to Deep Think via the Gemini app over the course of several days. For each problem, the evaluator recorded the full text of the response and saved the Python snippet in a stand-alone .py file for evaluation. The evaluator also took a screenshot showing that “Deep Think” mode was indeed selected in the app. These screenshots were checked by another evaluator. All work was conducted with Gemini set not to store data or use conversations to train models.

Deep Think does not always produce a response. In cases where it failed to respond, we retried up to ten times, stopping upon the first successful response. Of the 350 problems posed, nine failed to yield a response after ten tries.

Upon grading Deep Think’s responses, we noted several instruction-following issues:

• On ten problems, Deep Think failed to produce the requested Python snippet. Manually inspecting these, we found that, in four cases, it clearly had the correct answer.
• On six problems, there was a formatting issue where Deep Think had generated two identical or nearly-identical final-answer Python snippets, which failed to copy as valid Python out of the app. Manually correcting these we found that two returned the correct answer.
• On two problems, Deep Think returned the wrong answer type (e.g., SymPy expression instead of SymPy polynomial). In both cases it had the correct answer.
• Finally, on one problem, Deep Think generated a function that was not named answer, but the function it did generate yielded the correct answer.

For the problems where Deep Think clearly did have the right answer, we decided to mark it as correct. This is primarily because we were imposing the Python answer format only for our own convenience, and a manual grading against the standard of whether it gave the right answer in the chat would have marked these all as correct. In any case the ultimate difference was not large, adding eight correct answers (3%) to Tiers 1–3, and one correct answer (2%) to Tier 4.

Notes

1. We have not observed statistically significant performance differences from OpenAI models on the held-out vs. non-held-out problems. ↩

2. In one amusing case, a contributor stated that he believed a formula his problem relied on didn’t appear in the literature at all—only for an AI model to find the very formula in slides that the contributor himself had written and forgotten about. ↩

3. This sort of reasoning may well constitute the majority of human mathematical reasoning as well. ↩

4. This isn’t a super-secret held-out set: this problem variant arose due to what amounts to a mathematical typo in the original submission, changing the intended semantics of the problem. We only noticed this recently, so we happen to have evaluations on the typo variant of the problem for most models. GPT-5 Pro and Grok 4 Heavy also solve this problem. No model solves it with perfect reliability. ↩

5. It had in fact been solved by the initial run of Gemini 2.5 Pro, though we failed to notice this at the time. ↩

6. In one case, Deep Think claimed that there was a known counterexample to a particular conjecture, and attributed this to two of Ivanisvili’s collaborators on the topic. At least for Ivanisvili, this false citation was easier to spot. ↩

7. This also contrasts unfavorably with the reports of the mathematicians we commissioned to investigate Grok 4’s capabilities, both of whom reported Grok 4 to be particularly strong in this area. Note, however, that these were not the same mathematicians and they were not asking the same questions, so the contrast remains anecdotal. ↩

8. In addition to Google, this was also achieved by models from OpenAI and Harmonic. ↩

9. The first problem is a 35 “tough” and the second is a 40 “hard” on Evan Chen’s MOHS scale. These scores fall in between the 25 “medium” and 50 “brutal” scores assigned to the hardest two problems on the 2025 IMO. ↩

10. A full solution can be found on page twelve of Evan Chen’s IMO 2024 solution notes. ↩

11. Only 1% of contestants received full marks on this problem. Among the problems solved by AI on the 2025 IMO, the one solved by the smallest proportion of contestants was still solved by 16%. This problem was also ranked higher by US IMO coach Evan Chen on his Math Olympiad Hardness Scale than any of the AI-solved problems on the 2025 IMO: 40 vs. ≤ 25. ↩

12. We’ve written before that AlphaProof’s solution was particularly uninspiring, amounting to a low-level case-by-case analysis as opposed to a more conceptual argument like what a human would produce. But, being in Lean, it is nonetheless accurate. ↩

13. One oddity is that “aquaesulian” is not a term of art in math. It was coined in this very problem: the 2024 IMO took place in Bath, UK, the Roman name for which was Aquae Sulis. If Deep Think had used web search, it surely would have found this, but apparently it did not. ↩

14. More specifically, we’re referring to geometry problems of the sort found in high school math competitions such as the AIME or IMO. ↩

15. Recall that the Deep Think we are evaluating here is a variation of Google’s IMO gold model. ↩

16. As noted above, the Head of Science and Strategic Initiatives at Google DeepMind stated that data generated by AlphaProof was used to train Deep Think. We are not aware of as explicit a confirmation that the same is true for AlphaGeometry. ↩

17. OpenAI’s solution was noted for its extremely telegraphic writing style, but the point we are making here is solely about its mathematical content. ↩

18. Or, at any rate, it seems like a responsible solution should at least mention that it is slightly overloading one of the trucks, if that is what it suggests doing. ↩

19. More information about this scaffold can be found on our page about the FrontierMath benchmark. ↩