Evaluating Grok 4’s math capabilities
It’s good at involved computations, improving at proofs from a low base, and useful for literature search. It still favors low-level grinds and leans on background knowledge.
Published
xAI commissioned Epoch AI to evaluate Grok 4’s math capabilities. What are its strengths and weaknesses, absolutely and relative to other models? This report goes beyond headline numbers, aiming to characterize how Grok 4 approaches mathematical tasks. Such qualitative investigation informs a broader understanding of progress: it helps identify signs of novel capabilities before they show up in headline numbers, and suggests additional benchmarks that would be useful going forward.
Note: while this work was compensated, Epoch maintains full editorial control over the output. We offer timely and in-depth evaluation as a service to model developers; email info@epoch.ai for details.
Executive Summary
- Grok 4 is state-of-the-art at “grinding out” solutions on medium-hard high school math competitions. (link)
- Grok 4 is near the state-of-the-art at solving proof-based problems from challenging high school math competitions, though much headroom remains on proofs in general. (link)
- Professional mathematicians say Grok 4 may be the best available model for mathematical literature search. (link)
- Grok 4 shows an interesting tendency to catch some, but not all, of its own mistakes. (link)
- Like all LLMs, Grok 4 doesn’t reason in a particularly human way: it favors low-level calculation, lacks spatial intuition, and doesn’t exhibit much of what humans would call creativity. (link)
I also think some of the performance charts shown in the Grok 4 release blog post were misleading, though these points do not undermine the overall conclusion.
- Two competitions, the AIME and HMMT, should not have included a Python tool setting as these competitions are meant to be taken “by hand”. (link)
- xAI internally graded another competition, the USAMO, without much transparency. While this practice is common, it makes comparison difficult. (link)
I’ll use the rest of this post to flesh out and justify these conclusions.
Methodology
Data. This post draws from three primary data sources. First, I consult standard benchmarks to contextualize Grok 4’s place on the field overall. I also delve into specific example problems from benchmarks in order to show more concretely how Grok 4 does and does not solve problems. Second, I use some problems I’ve collected from my personal blog, which are complementary to benchmark problems. Third, I incorporate the commentary of two professional mathematicians, Greta Panova and Bartosz Naskręcki, whom Epoch contracted with to provide their impressions after using Grok 4.1
Models. xAI offers two variants of Grok 4: the standard model and Grok 4 Heavy. xAI describes Grok 4 Heavy as “deploying several independent agents in parallel to process tasks, then cross-evaluating their outputs”. I investigate both, though my access to Grok 4 Heavy is somewhat limited: there is no API, and the model available on grok.com is highly inclined to search the web. This means it often finds write-ups of problems that I want to see if it can solve “on its own”. xAI suggested that sampling Grok 4 via the API several times and looking at the best solution would be a rough approximation for Grok 4 Heavy’s capabilities. In the end, I don’t think this limitation significantly hampered my investigations.
Limitations. This analysis focuses only on math capabilities that I believe we can productively assess with the available data. In general, AI evaluations have a ways to go before they can cover all relevant aspects of any complex human endeavor. Math is no exception. For example, we are not able to measure a model’s ability to engage in such mathematically critical activities such as making interesting conjectures, generalizing existing results, or applying techniques from one field to a superficially unrelated field.
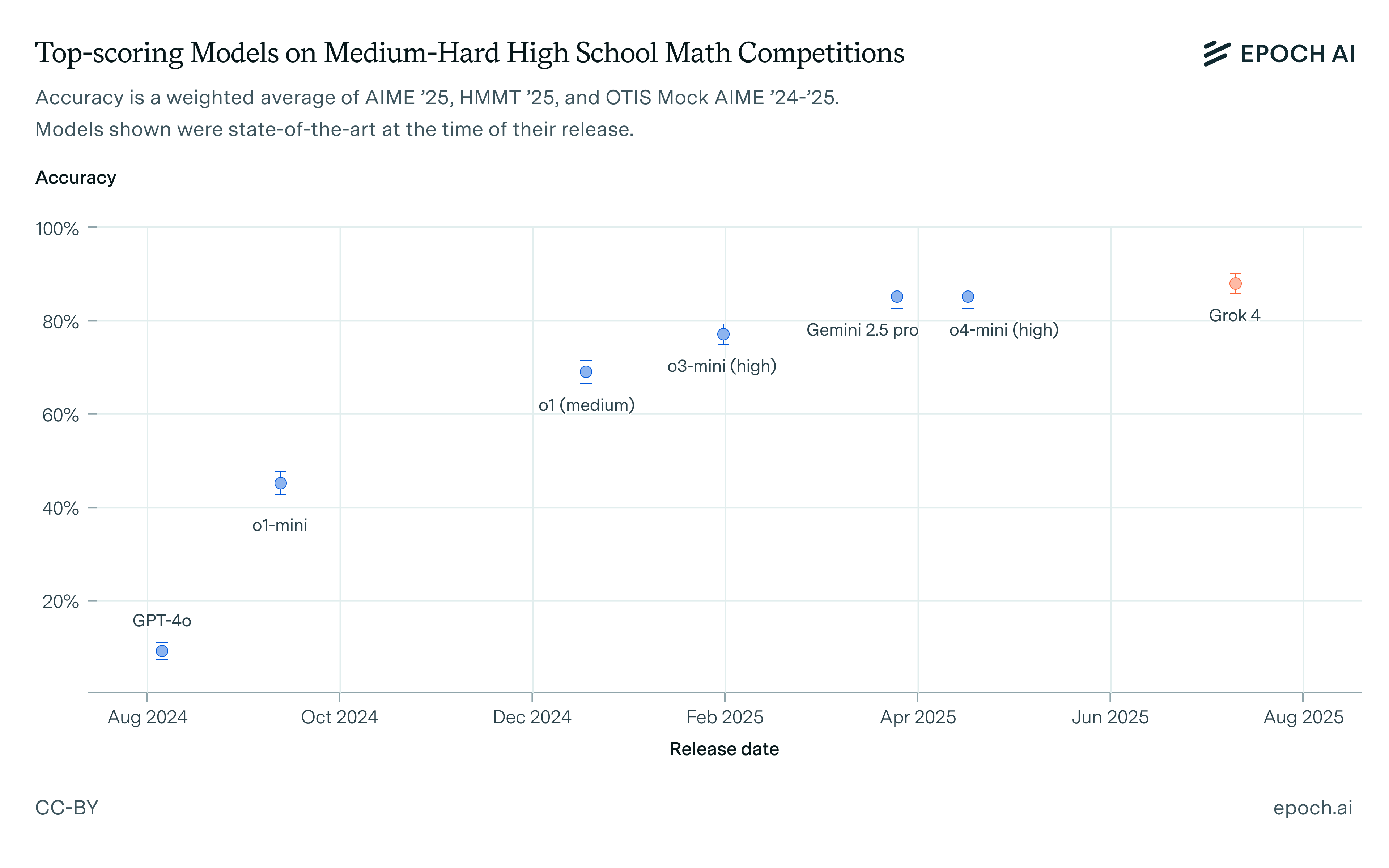
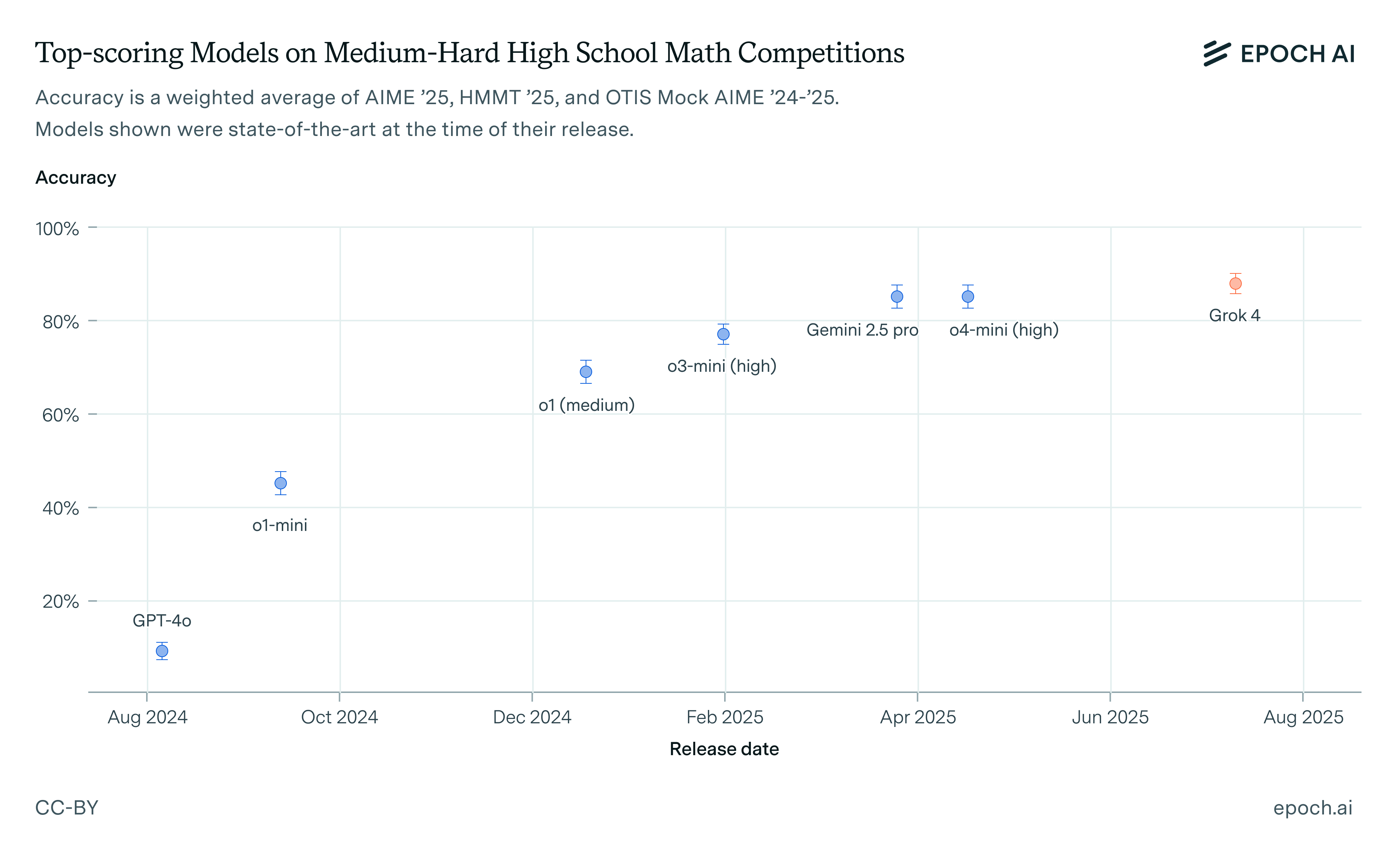
Grok 4 is state-of-the-art at “grinding out” solutions on medium-hard high school math competitions
For this section, I’ll draw from three high school math competitions that are now used as AI benchmarks: the AIME, HMMT, and OTIS Mock AIME.
On a rough 1–10 difficulty scale, where 1 is an easy word problem and 10 is the hardest problem ever given on any high school math competition, problems from these competitions fall in the 2–6 range and cluster toward the upper end of that range. I thus refer to them as “medium-hard”. I use data from independent evaluations conducted by MathArena and Epoch.2
| Competition | Years | Benchmarker | Difficulty (1-10) |
|---|---|---|---|
| AIME | 2025 | MathArena | 2-6 |
| HMMT | 20253 | MathArena | 5-6 |
| OTIS Mock AIME | 2024, 2025 | Epoch AI | 2-6, skewed harder |
A year ago, LLMs could only solve the easiest of these problems. Since then, reasoning models have made rapid progress. The chart below shows a composite score on these benchmarks for models that were state-of-the-art at the time of their release. The previous state-of-the-art is a tie between Gemini 2.5 Pro and o4-mini (high) at 85%. Grok 4 scores 88%, representing a small step forward.
I’ll now give a qualitative sense of what it takes to solve these problems and how LLMs do it. I’ll review solutions to one problem that most frontier models can solve, one problem that (so far) only Grok 4 has solved, and one problem that no model has yet solved.
Solving these problems requires moderate knowledge and high diligence
These competitions require high proficiency with an advanced high-school math curriculum and the ability to carry out fairly involved calculations. For humans, competition time constraints are especially binding: success hinges on quickly recognizing the right approach and then executing it correctly on the first try.
The highest-scoring humans can find clever shortcuts which allow them to solve problems without having to spend as much time chugging through equations. This is the only role that creativity, cleverness, and novelty play in these competitions.
To-date, LLMs have uniformly tended to take a “grind it out” approach, and Grok 4 is no exception.4 Its improvement over other models on these benchmarks reflects an ability to carry out more involved grinds with greater reliability.
What does it look like to “grind out” a problem?
Here is Problem 9 from the 2025 AIME, which all frontier models, including Grok 4, solve reliably. I’ve lightly rewritten it for readability.
The parabola with the equation y = x² – 4 is rotated 60° counterclockwise around the origin. Find the coordinates of the point in the 4th quadrant where the original parabola and its image intersect.
The chart below shows the two parabolas and the point of interest.
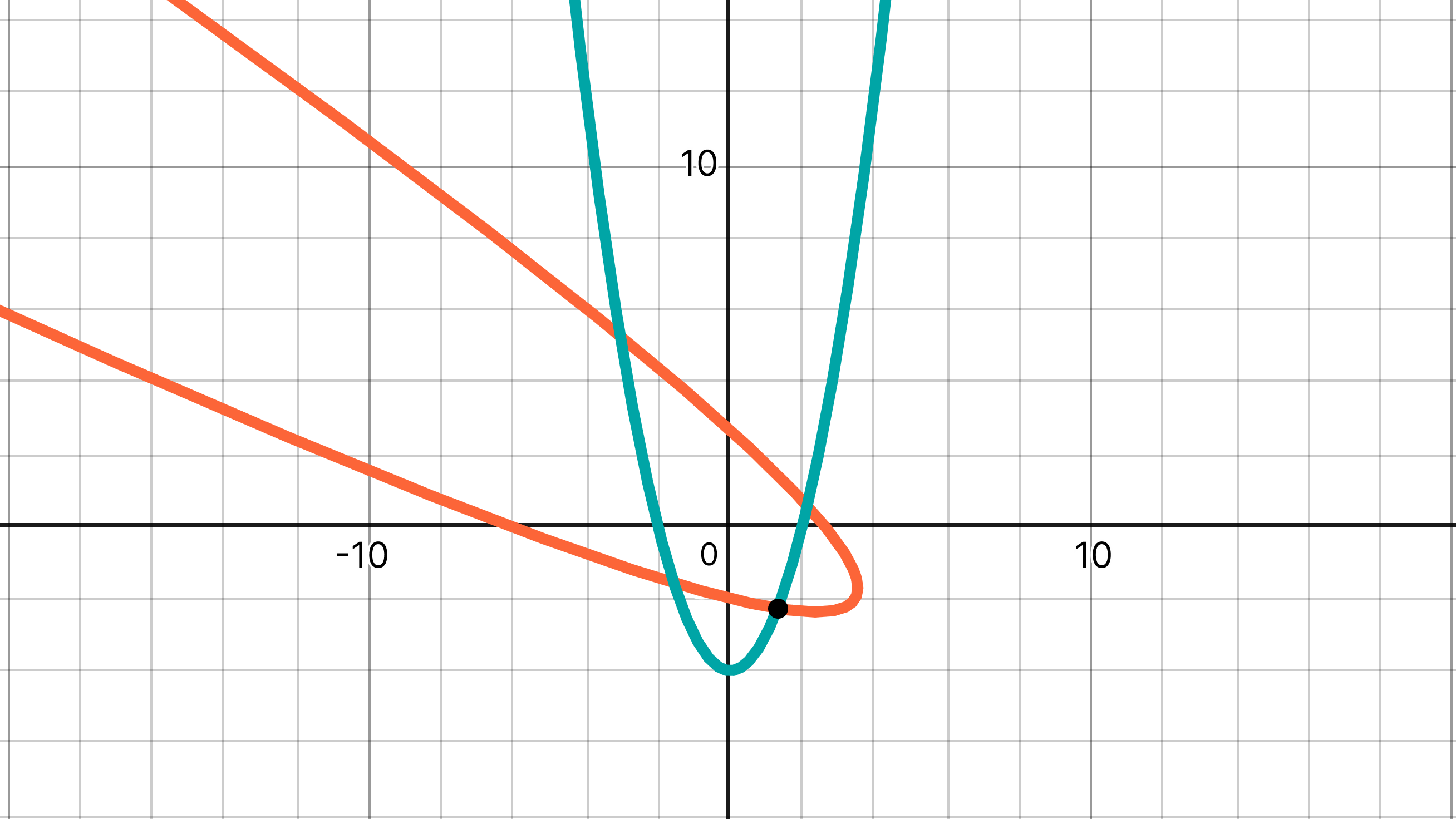
Here is an outline of how LLMs, including Grok 4, solve this problem.
- Apply the relevant rotation formula to y = x² – 4 (the teal parabola).
- This yields x² + 2√3 xy + 3y² + 2√3 x – 2y – 16 = 0 (the orange parabola).
- Substitute in y = x² – 4, yielding 3x⁴ + 2√3 x³ – 25x² – 6√3 x + 40 = 0.
- Solve that quartic equation.
LLMs roll up their silicon sleeves and get it done. Clever humans, however, can find something better:
- The 60° rotation is, in this case, equivalent to reflecting through the line x = -y/√3.
- Thus, we actually only need to find the intersection between that line and y = x² – 4.
The difference in this case between the “grind it out” and the “clever” solution isn’t enormous, but it can grow significantly for even modestly harder problems.
Grok 4 is at the frontier of “grinding out” problems
Overall, Grok 4’s progress in this category reflects an ability to grind out more problems and to do so more reliably. For example, below is Problem C9 from HMMT. Grok 4 is the first model evaluated by MathArena to solve this problem.
Two points are selected independently and uniformly at random inside a regular hexagon. Compute the probability that a line passing through both of the points intersects a pair of opposite edges of the hexagon.
The human reference solution for this problem is quite nice. I’ll include most of it as images, but you can get the gist just by reading my brief commentary before each image.
First, solve a similar problem for triangles. The answer is independent of the shape of the triangle!
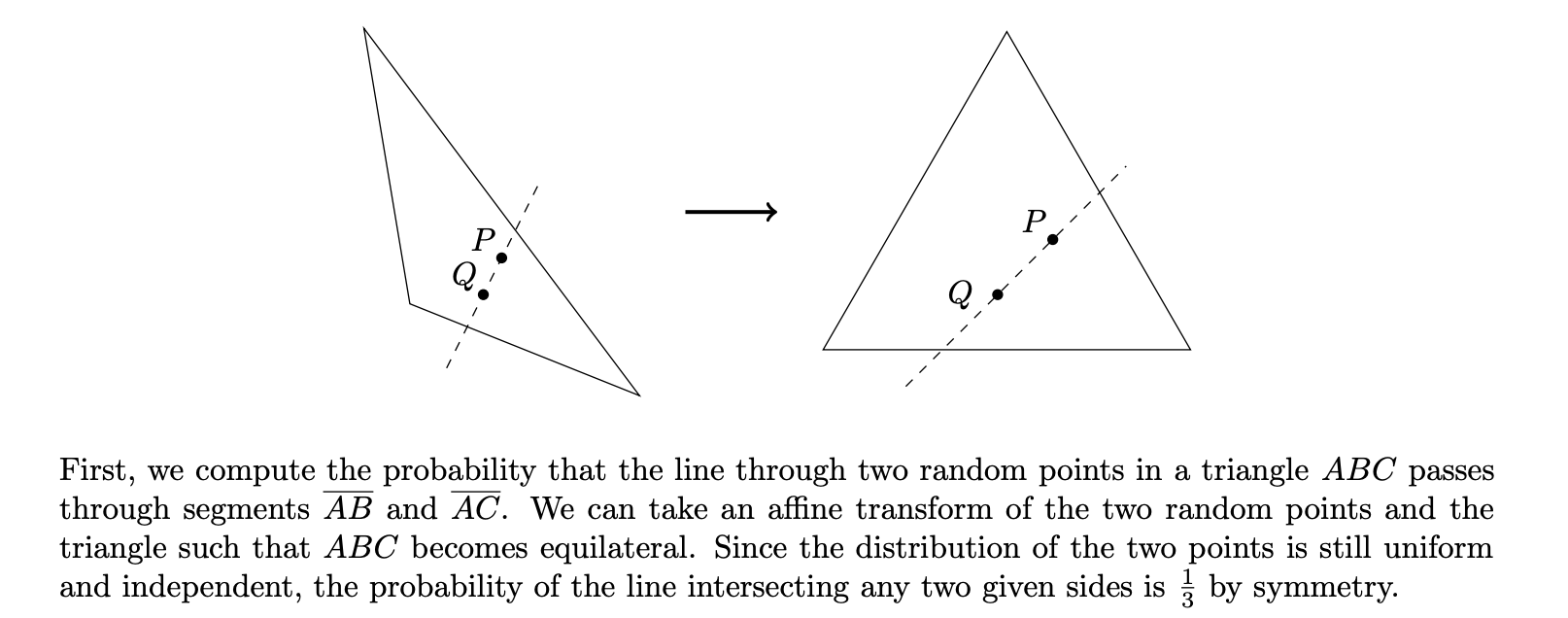
Then, use this to solve a similar problem for rectangles. Again the answer doesn’t depend on the rectangle’s dimensions.
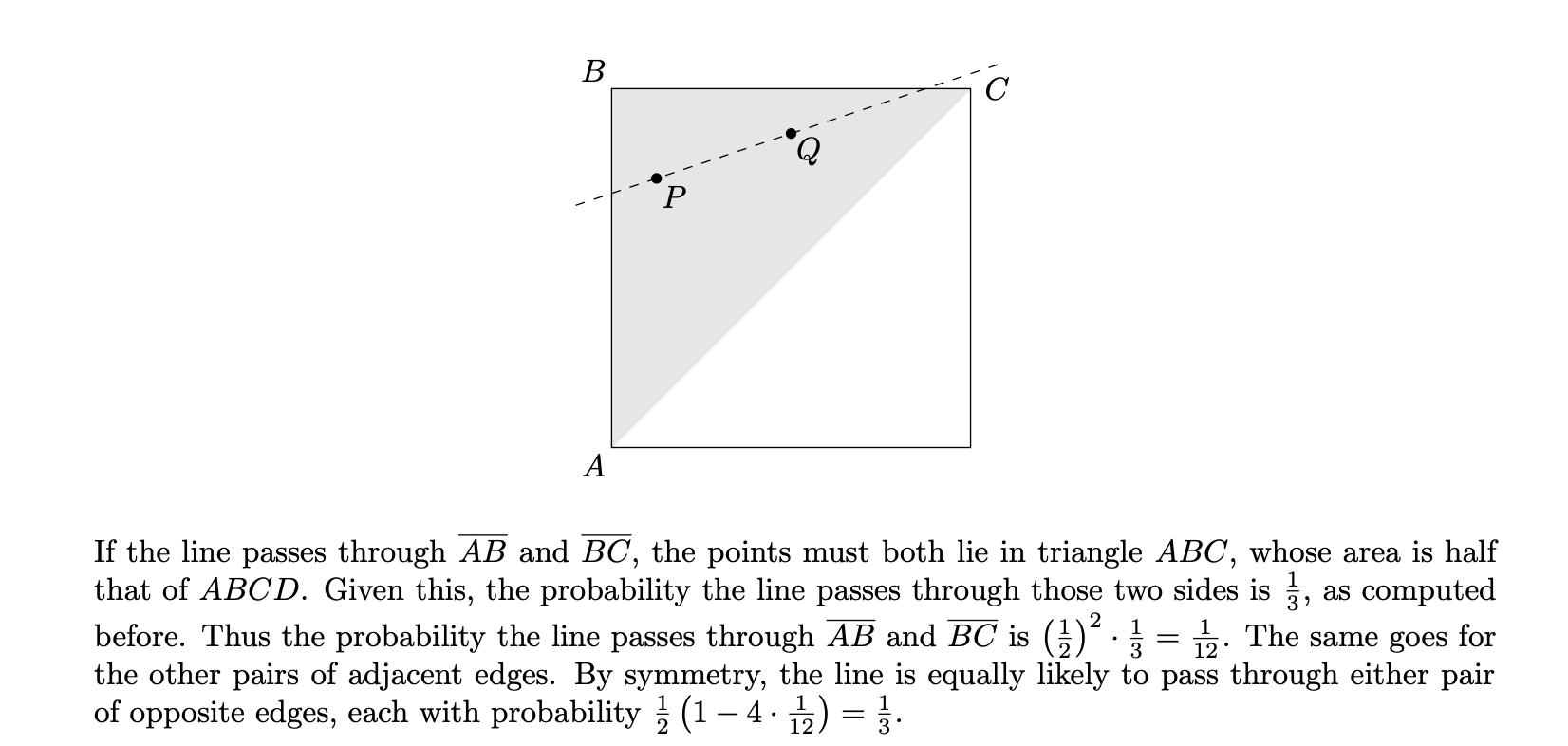
Finally, extend this to the desired case of the hexagon.
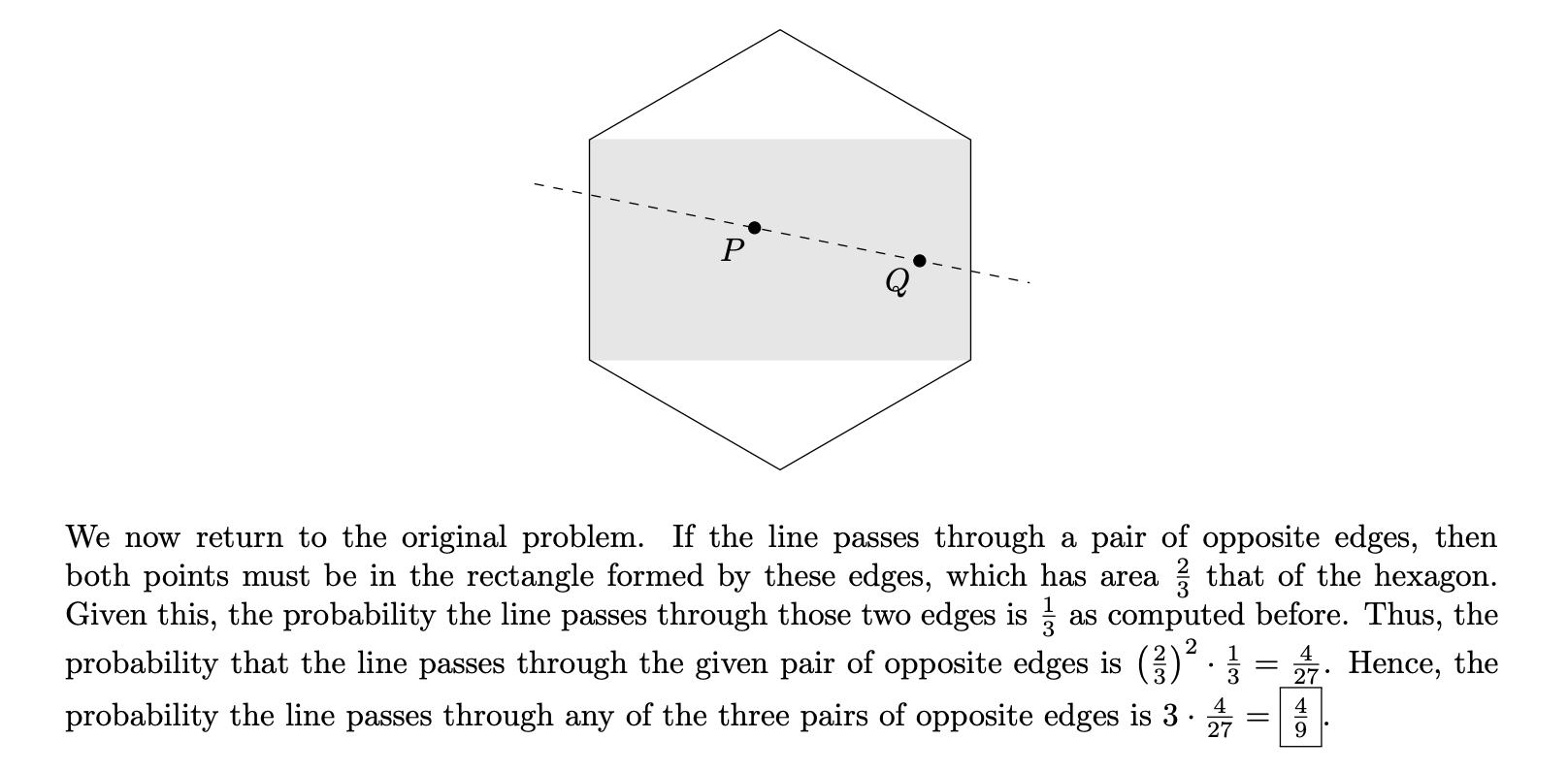
This is not easy for a human to come up with, but it’s certainly “elegant”: not only is it concise, but it gives a feel for what’s going on more deeply than just the specific instance.
Grok 4 solves this problem differently. Here is a representative sample, though I suggest you skim it. The upshot is that Grok 4 places the hexagon in the Cartesian plane, considers the space of lines parametrized in four-dimensional space (two coordinates for each line), and uses a quadruple-integral to find the (hyper)volume representing the final answer.

This isn’t a bad solution! The whole point of Cartesian coordinates and calculus is to augment the subtler, more conceptual arguments found in classical geometry with something more rigorous and replicable. A human on the actual HMMT probably wouldn’t have time to execute Grok 4’s solution here, but in some ways Grok 4’s solution is more of a sure thing. Grinds are good, if you can get them. For this class of problem, you usually can.
While a few problems on these competitions remain unsolved by AI, that probably won’t remain the case for long
There are 105 problems in these three benchmarks combined. Only 4 of them have yet to be solved even once by any model, according to MathArena’s and Epoch’s data. Here’s an example of one of these, OTIS Mock AIME 2024 Problem 14.
Ritwin the Otter has a cardboard equilateral triangle. He cuts the triangle with three congruent line segments of length x spaced at 120° angles through the center, obtaining six pieces: three congruent triangles and three congruent quadrilaterals. He then flips all three triangles over, then rearranges all six pieces to form another equilateral triangle with an equiangular hexagonal hole inside it, as shown below. Given that the side lengths of the hole are 3, 2, 3, 2, 3, 2, in that order, find x.
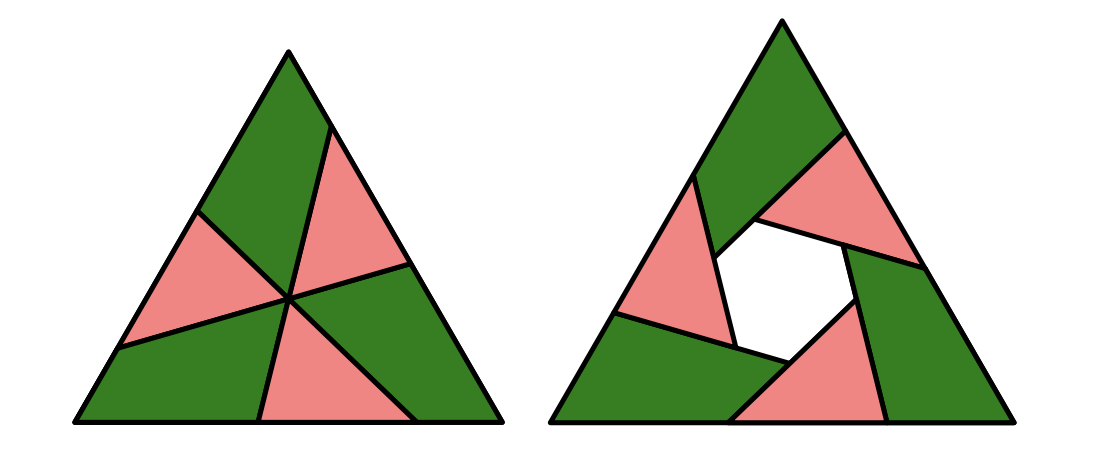
The human reference solution isn’t that conceptual. It labels the diagram as shown below, and then uses standard geometry facts to deduce five relationships among a, b, c, d, and e. Then it’s just a matter of solving the resulting system of equations.
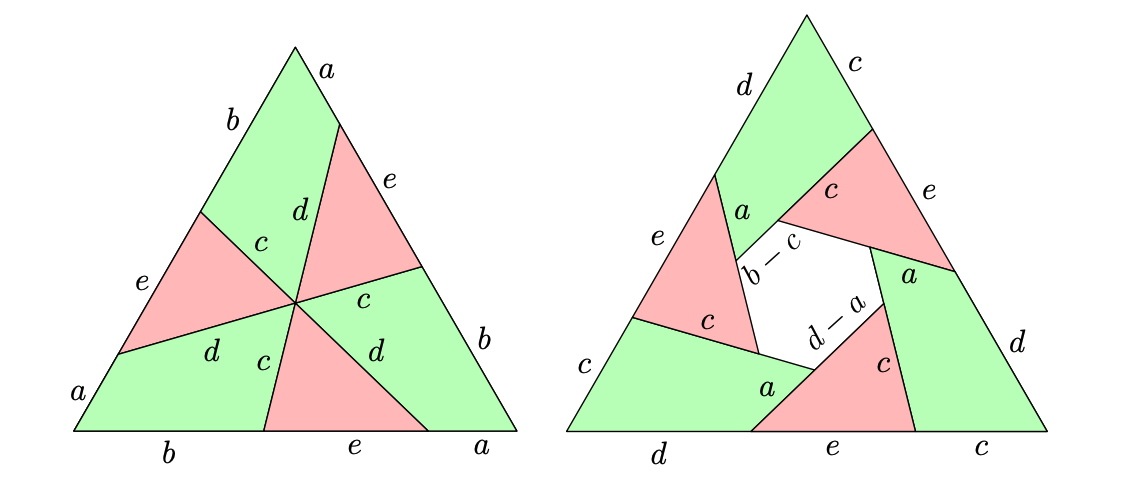
What seems to make this hard for LLMs is that casting it as a grind-able problem requires some pretty intricate work with coordinates. That is, figuring out the coordinates of the vertices of the second shape, after flipping the triangles and rearranging everything, would require a very lengthy computation. Still, it’s qualitatively similar to what they’re already doing, so I expect it to be just a matter of scale before one of them solves it.
This class of problem is very nearly saturated. Going forward, the most interesting thing we can learn from such benchmarks is whether models start to solve problems in more conceptual ways.
Disregard Settings Involving Coding Tools
xAI’s blog post reports higher scores on AIME and HMMT if Grok 4 is given access to a Python tool. This is not an appropriate setting for these competitions: the problems are designed to be solved “by hand” and are not intended to remain challenging if coding is allowed.
For example, here is Problem 15 from the 2025 AIME, another one of the 4 problems that no model has yet solved.
Find the number of ordered triples of positive integers (a, b, c) such that a, b, c ≤ 3⁶ and a³ + b³ + c³ is a multiple of 3⁷.
This is easy to solve with a Python script, but much more difficult without.5
Grok 4 is near the frontier of solving proof-based problems, but much headroom remains
In this section, I’ll look at two more challenging high school math competitions, as well as comments from professional mathematicians.
I’ll start by considering two competitions of similar difficulty and format: the USAMO and the IMO. These are as hard as any high school math competition gets. On the same 1–10 difficulty scale, their problems fall in the 7–9 range. Specifically, there are usually two 7s, two 8s, and two 9s on each competition each year.6 I’ll refer to these as the “easy”, “medium”, and “hard” problems respectively.7
| Competition | Years | Benchmarker | Difficulty (1-10) |
|---|---|---|---|
| USAMO | 2025 | MathArena, Companies | 7–9 |
| IMO | 2025 | MathArena, Companies | 7–9 |
Whereas the problems on the benchmarks discussed earlier have short-form answers, the problems on the USAMO and IMO require rigorous proofs. In the competitions, solutions are graded by human experts on a 0-7 scale, with 0 corresponding to no progress and 7 corresponding to a complete solution. Partial credit is awarded sparingly: usually 1–2 points for meaningful steps that are still far from a solution or 5–6 points for a nearly complete solution that has at most small flaws.
Self-Reported Grading Makes Interpretation Harder
The ideal grading format on such competitions is third-party graders using a standardized rubric, and grading “blind”, i.e., not knowing which model wrote which solution. This is precisely what MathArena does. However, when companies self-report internally graded results, comparison becomes more difficult. In particular, internal graders may be using different rubrics and may have different standards for awarding partial credit. Failing third-party grading, we would at least know more if companies preregistered a grading guide and then published their models’ solutions and scores.
xAI self-reported results on the USAMO, so we must keep the above in mind as we interpret these results. These remarks are not meant to cast aspersions on xAI specifically: no company today meets the above standard.8 Indeed, there’s a great opportunity for a provider to distinguish themselves by being the first to start operating this way!
Solving these problems requires deeper mathematical skills
These competitions require proficiency with the same advanced high-school math curriculum mentioned earlier. They also require rigorous argument: proofs must be constructed carefully, without logical gaps.
The easier problems don’t require much more than that. I would characterize the harder problems as adding three additional factors: abstraction, creativity, and depth. Abstraction refers to the need to derive general truths about the subject of the problem, not just chug through formulas. Creativity refers to the need to come up with something new, not just straightforward application of background knowledge. Depth refers to the number of steps required to carry out a solution. Of course, these factors can combine: the very hardest problems require many steps, each of them involving a novel abstraction.
To-date, LLMs have not done well on harder instances of these problems. This is likely because it’s less clear how to do reinforcement learning (RL) on problems where there isn’t an easily-verifiable answer, and natural-language proofs are not easily verifiable.
Grok 4 Heavy made novel progress on a challenging USAMO problem, thanks in part to its background knowledge
xAI’s most notable claim was that Grok 4 Heavy scored 62% on the 2025 USAMO. The xAI team shared with Epoch that this corresponded to solving the two “easy” problems and one of the medium problems reliably, while achieving partial credit (in the 5–6 point range) on the two “hard” problems some of the time. Prior to this, publicly available models had only solved the two “easy” problems, and Google’s not-yet-available Gemini 2.5 Pro Deep Think system had solved the same “medium” problem.910
xAI also shared with us its top-rated solutions for this medium problem and the two hard problems. The solution to the medium problem is substantially similar to Deep Think’s. This is already notable in that Deep Think had been the only model to solve this problem.
But, in terms of demonstrating novel capabilities, the two hard problems are of more interest.
Here’s the first of the two hard problems, though feel free to skim it, as the discussion won’t depend on understanding it deeply.
Alice the architect and Bob the builder play a game. First, Alice chooses two points P and Q in the plane and a subset S of the plane, which are announced to Bob. Next, Bob marks infinitely many points in the plane, designating each a city. He may not place two cities within distance at most one unit of each other, and no three cities he places may be collinear. Finally, roads are constructed between the cities as follows: for each pair A, B of cities, they are connected with a road along the line segment AB if and only if the following condition holds: For every city C distinct from A and B, there exists R in S such that △PQR is directly similar to either △ABC or △BAC. Alice wins the game if (i) the resulting roads allow for travel between any pair of cities via a finite sequence of roads and (ii) no two roads cross. Otherwise, Bob wins. Determine, with proof, which player has a winning strategy.
Note: △UVW is directly similar to △XYZ if there exists a sequence of rotations, translations, and dilations sending U to X, V to Y, and W to Z.
I’ve previously noted that this problem draws from some established areas of mathematics. The winning strategy for Alice is to choose S so that the resulting graph of cities is what’s known as a Gabriel graph. It’s not necessary to know about Gabriel graphs to solve the problem, and probably no contestants had this knowledge. But LLMs certainly do! Prior LLM attempts on this problem have indeed tried to make use of established facts about Gabriel graphs, though these attempts didn’t pan out.
Grok 4 Heavy’s solution also uses Gabriel graphs, and it gets further than other models did. It’s not logically complete: I spot at least one mistake, where it makes an inference that is only valid if Bob places a finite number of cities, not an infinite number. But, even if the overall solution deserves partial credit, I think that credit is more a reflection of its mastery of background knowledge than its ability to find novel ways to solve problems.
I think Grok 4 Heavy’s solution to the second problem is weaker. Here’s the problem:
Let m and n be positive integers with m ≥ n. There are m cupcakes of different flavors arranged around a circle and n people who like cupcakes. Each person assigns a nonnegative real number score to each cupcake, depending on how much they like the cupcake. Suppose that for each person P, it is possible to partition the circle of m cupcakes into n groups of consecutive cupcakes so that the sum of P’s scores of the cupcakes in each group is at least 1. Prove that it is possible to distribute the m cupcakes to the n people so that each person P receives cupcakes of total score at least 1 with respect to P.
Grok 4 Heavy converts this to a geometric context, where points in space represent an assignment of cupcakes to people. In working from there, it incorrectly applies a theorem from geometry. What it actually proves is that there’s a way to assign fractions of cupcakes to people that satisfies the desired property. But the problem asks for cupcakes to be assigned whole, and I don’t know if there’s a way to repair Grok 4 Heavy’s solution. Again, I’m not deeply familiar with the partial credit standards of the USAMO, but I would be inclined to grade this solution more harshly.
Where I net out is that Grok 4 Heavy’s progress on the USAMO amounts to an improvement in proof-writing ability at very least comparable to Gemini 2.5 Pro Deep Think’s, plus an improved ability to marshal background knowledge in such proofs.
Grok 4 did not shine on the 2025 IMO
Here we get MathArena’s blind third-party grading following a standardized rubric. Unfortunately, there are quite a few caveats to this. My tentative conclusion is that Grok 4 did not do well out of the box, but that elicitation appears to matter so much that I wouldn’t be surprised if we saw rapid near-term improvement.
The first caveat is that MathArena can only evaluate Grok 4, not Grok 4 Heavy, since the latter doesn’t have an API yet. But it was Grok 4 Heavy which claimed the most interesting proof-based results on the 2025 USAMO.
I think this isn’t such a complication: MathArena used a best-of-n elicitation strategy which should somewhat approximate Grok 4 Heavy’s architecture. From their blog post:
We applied a best-of-32 selection strategy using a method based on previous work. In our prior work, we found that this method works very well for proof generation tasks, almost doubling performance of the models on the data we had at hand. Specifically, for each model solution, we first generated 32 responses. These responses were evaluated in a bracket-style tournament using an LLM-as-a-judge system to select winners in head-to-head comparisons. Here, the model itself was used to evaluate its own responses. The model judged each pair and selected the stronger response. This process was repeated until a single best response remained which was then presented to the human judges for evaluation.
Even so, Grok 4 performed poorly—but in a surprising way. MathArena noted:
Grok-4 significantly underperformed compared to expectations. Many of its initial responses were extremely short, often consisting only of a final answer without explanation. While best-of-n selection helped to filter better responses, we note that the vast majority of its answers (that were not selected) simply stated the final answer without additional justification.
The xAI team found that a short prompt, which had been used in Grok 4’s training, elicited significantly longer answers which, at least superficially, better resembled proofs. MathArena decided to conduct a second evaluation of Grok 4 using this prompt. Of course, this is no longer an apples-to-apples comparison, but MathArena felt that, with transparency, it was useful information to share with the research community. You can read their full reasoning here.
The table below shows results for both Grok 4 runs, plus initial results for other models.
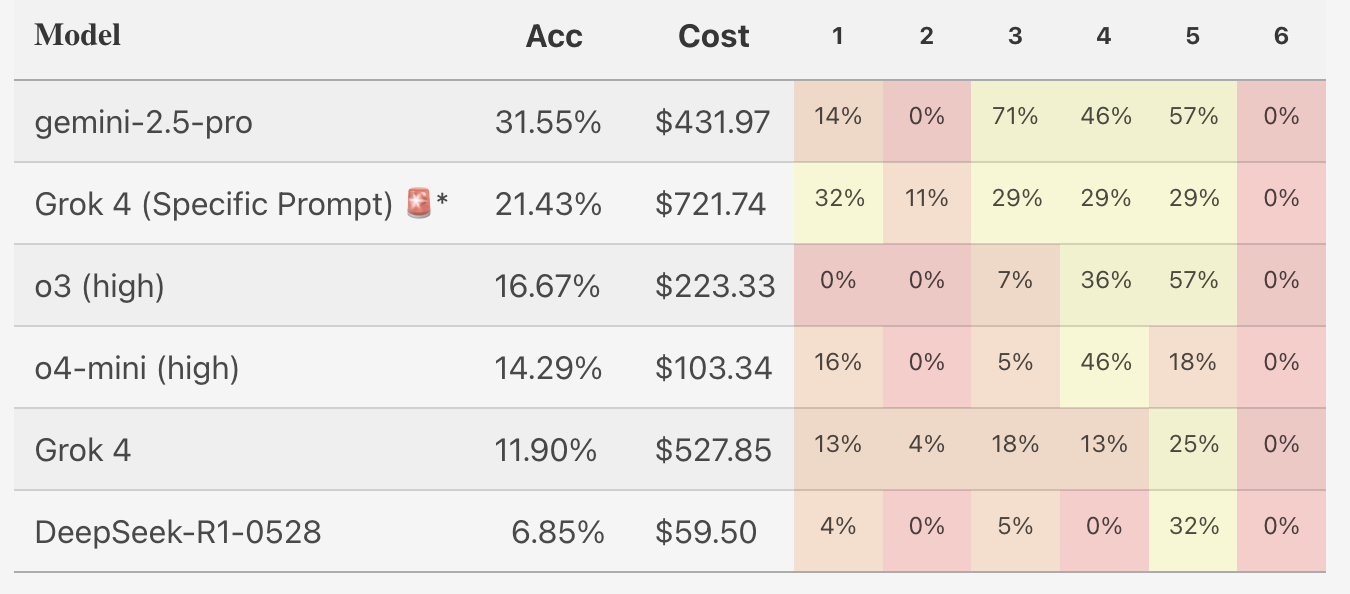
I think this doesn’t complicate our conclusion too badly either. Whether its score is 12% or 21%, we can say that Grok 4 is not doing well on the IMO in this setting. Furthermore, Grok 4’s performance, even with the modified prompt, is entirely due to partial credit: its highest score on any single sample is 3/7. If a human got such scores, I would take that to mean that they didn’t really know how to solve the full problems. This is bearish for Grok 4, although most models do poorly by this metric: Gemini 2.5 Pro is the only model here to score 7/7 on any problem, achieving that on 2/4 samples for Problem 3.
Finally, there have been notable announcements of results not evaluated by MathArena. Google and OpenAI announced much higher performance on the 2025 IMO from unreleased, experimental systems: equivalent to 83.33% if placed on the table above. But also, Lin Yang, a professor at UCLA, claimed to have evoked identical performance from the publicly-available Gemini 2.5 Pro using only prompting and scaffolding: no experimental training required.
While I haven’t verified Yang’s results in depth, they seem entirely plausible to me. That is in part because, somewhat unfortunately for AI evaluation purposes, the first 5 problems on this year’s IMO turned out to be unusually easy, at least according to expert human ratings. According to these ratings, the 2025 USAMO problem that Gemini 2.5 Pro Deep Think and Grok 4 Heavy both solved was harder than any of the first 5 problems on this year’s IMO.
Where does this leave us? I think we can safely conclude two things.
First, out of the box, Grok 4 did not shine on the IMO. This doesn’t put it in terrible company, but also puts an upper bound on its capabilities.
Second, elicitation matters. LLMs in general clearly have some of the raw material for solving proof-based problems, but still struggle to put it all together. (This, at least, isn’t completely new: I’ve been writing about it since March.) Given that, we can probably expect a solidification of these latent capabilities in the near-term, at which point models may solve easy-to-medium olympiad problems more reliably. Whether Grok leads or lags here remains to be seen.
Mathematicians say Grok 4’s proof-writing abilities are hit or miss
If Grok 4 has made progress on proofs, it is only incremental. The two mathematicians we consulted found Grok 4 on par with other leading models such as Gemini 2.5 Pro and o4-mini-high, but overall judged Grok 4’s facility with proofs to be inadequate for research-level math.
Panova found Grok 4 to be especially weak in her specialty of algebraic combinatorics. Grok 4 did not “seem to understand the level of detail required” by a working mathematician for a proof. Naskręcki noted that Grok 4 prefers very short answers. Even when coaxed to provide its justification for a given conclusion, its reasoning is often “full of gaps”.
Panova also reported that Grok 4, like all LLMs, would handwave its way through proofs that required rigorous but “soft” arguments, i.e. arguments that mathematicians would find convincing even if they were mostly given in natural language as opposed to formal equations. She also noted that, a bit more idiosyncratically, Grok 4 often tried to prove things by mathematical induction, regardless of whether this was an appropriate technique.
Naskręcki found that Grok 4 could come up with very convincing-looking proofs that were nonetheless incorrect, and this can be a serious sidetrack for a working mathematician. Panova echoed this, noting that humans are often more upfront when they don’t have a correct answer.
I think these comments are not inconsistent with the benchmark results. Those competitions are challenging, and Grok 4 (like all models) hasn’t even mastered them yet. But real research math is in another league.
Sense Check: Grok 4 did fine on FrontierMath
Epoch’s FrontierMath benchmark gives us an independent data point on Grok 4’s overall math capabilities: while concerns about overfitting and data contamination may loom over public benchmarks, the private FrontierMath problems should be safe from that.
FrontierMath is designed to test for mathematical background knowledge, creative problem solving, and execution of involved computations. It differs from other math benchmarks primarily in difficulty, targeting advanced undergraduate to early-career research level problems. These problems would not appear on high school math competitions.
We have thus far run Grok 4 on FrontierMath’s Tier 1-3 problems twice, trying to find API settings that would let us get a complete run. Grok 4 scored 14% and 12% on these runs, which we consider to be statistically indistinguishable. This puts it ahead of all other models that we have run, except for o4-mini.11
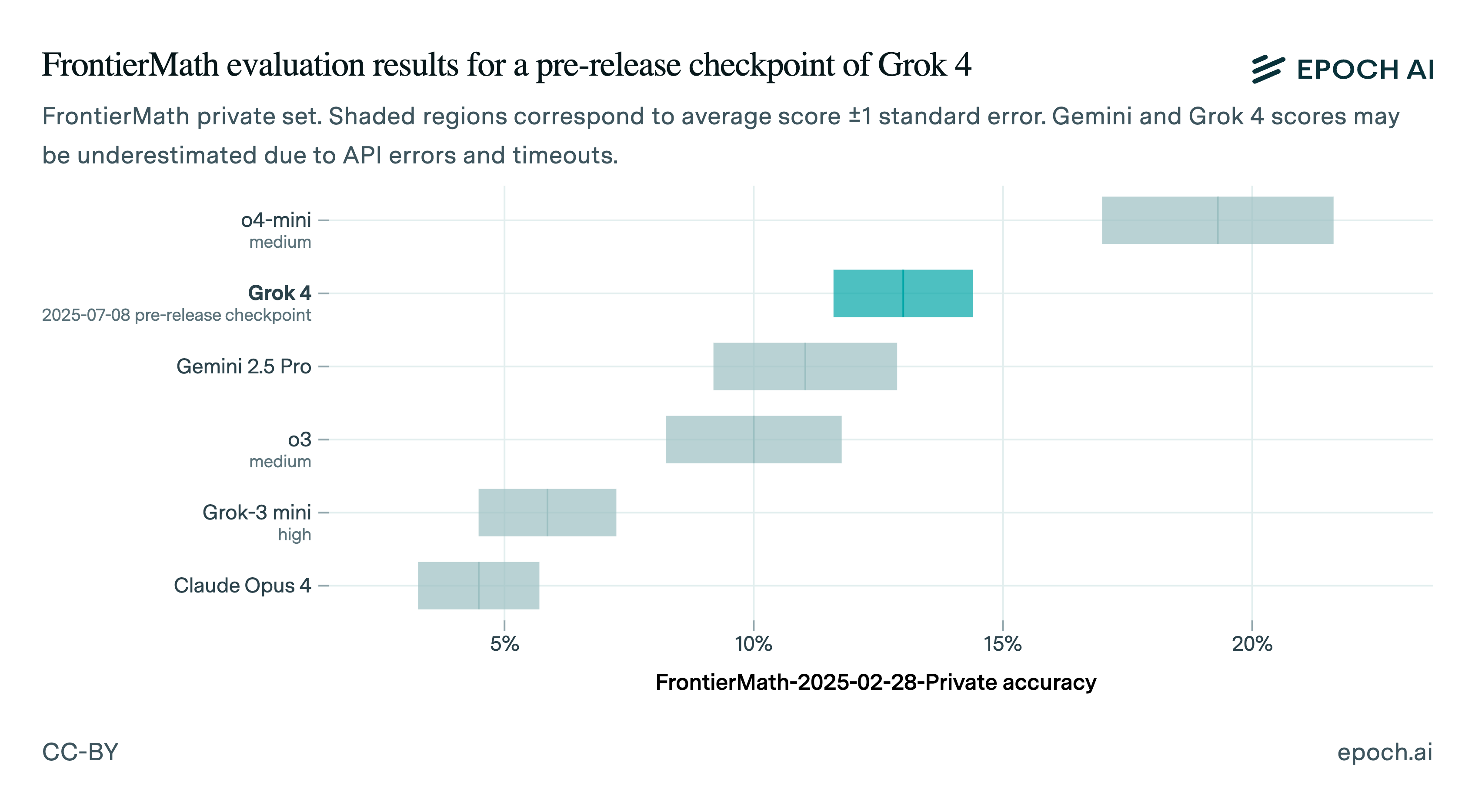
Overall we note that more models are hitting our scaffold’s total token limit of 100k, and we plan to run several frontier models again with increased limits. Also, given that mathematicians were impressed with Grok 4’s command of the literature, it will be interesting to run it with web search enabled. Our scaffold does not support that yet, but we plan to add it.
Across these two runs, Grok 4 solved 6 problems that no model we have run has solved before. It’s hard to say how much of this is just due to noise, but I buy the general pattern that Grok 4 has some unique problem-solving strengths that at very least mean no other model dominates it problem-by-problem.
Of the 48 more challenging Tier 4 problems, Grok 4 solved a single one. Other models had already solved this one. Overall, only three Tier 4 problems have been solved by any model.
Grok 4 is good at mathematical literature search
The mathematicians found Grok 4’s ability to search the mathematical literature to be very impressive. Consistent with our observations on the first of the two hard USAMO problems, Grok 4’s argumentation was improved when it could lean on the literature, and it was quite good at finding relevant sources.
Naskręcki described this as one of Grok 4’s biggest strengths. He said that Grok 4 “excels at web searches and source comparison” and thought that it seemed more mature as a product in this regard compared to other models. It might become his “go-to model for first search in the field, quickly finding a very extensive list of relevant literature”.
For example, Naskręcki asked Grok 4 to explain how to compute the étale cohomology of curves. It was able to draw all the relevant steps from the literature, and, he believed, would be a great starting point for an entry-level researcher getting up to speed.
Furthermore, when combined with literature search, Naskręcki was impressed with some of Grok 4’s computations. He asked it to compute the Cech cohomology of a torus, which “while not super hard, is particularly involved”. Grok 4 consulted the web for relevant material and was eventually able to piece the computation together. He also found it to perform well when structuring the relevant literature for computing the Mordell-Weil group of an elliptic curve over a function field, which is a very elaborate task. Providing a blueprint for such theoretical computations would be useful for researchers trying to prototype or test out theories. Grok 4 was notable, when compared to Gemini 2.5 Pro and o4-mini-high, for including much more relevant literature in its results. Naskręcki was also impressed with Grok 4’s tendency to explore its ideas, not just through repeated web search but also through writing small Python scripts.
Naskręcki summed it up as follows:
In literature searches, Grok 4 shines by quickly identifying relevant papers and connections across mathematical fields, helping me discover ideas and references I might have otherwise missed.
Panova reported much of the same. She found Grok 4 notable compared to other models for its tendency to try things out. It would work through small examples and search the web for applicable theorems. It sometimes found quite obscure, but correct, references. She found its computational abilities a bit more hit or miss. On one problem relevant to her research, Grok 4 retrieved obscure but relevant formulas from the web “which even experts might not know about”, but then miscalculated the final answer.
Panova summed it up as follows:
Grok4 spends a lot of time searching for answers in all possible directions returning the shortest possible response but spares you the details, mastering handwaving and proofs by intimidation. While it may confuse itself from too much thinking, its search leaves no internet stone unturned and finds well hidden references.
Overall Grok 4 felt highly exploratory to both. Perhaps relatedly, both also noted that Grok 4 took longer to respond than other leading models.
Panova also found that Grok 4’s tendency to search in many directions could lead it astray. Especially for “camouflaged” problems, where the setup could obscure the fundamental subject matter, Grok 4 would go down many dead ends, “looking for significance and hints in every direction”. Naskręcki found much the same, noting that when problems become very difficult, Grok 4 would start many searches in many directions but have “no clear policy or strategizing”. Naskręcki thought features where the user could intervene on the search and provide guidance would be helpful.
Grok 4 shows a tendency to catch its own mistakes
Here I’ll review two elementary problems I have previously explored on my blog, notable for the fact that many frontier models get them wrong, despite their simplicity.
Grok 4 gets my favorite “trick” question
GSM8K is a benchmark of simple, grade-school level word problems that has long since been nearly saturated, but never quite 100%. Thanks to PlatinumBench, we can see which GSM8K problems frontier models still get wrong. I think many of these them come down to ambiguous wording, but one stood out as different:
A landscaping company is delivering flagstones to a customer’s yard. Each flagstone weighs 75 pounds. If the delivery trucks can carry a total weight of 2000 pounds, how many trucks will be needed to transport 80 flagstones in one trip?
As I’ve discussed, almost all frontier models get this wrong. I got it wrong myself at first. If you do 80 flagstones times 75 pounds you get a total weight of 6000 pounds. It seems like that fits neatly onto 3 trucks. But wait, how many flagstones can actually fit on a single truck? 26 flagstones would weigh 26 x 75 = 1950. With a truck capacity of 2000, there wouldn’t be room for a 27th. But if each of 3 trucks carries 26 flagstones, that only accounts for 3 x 26 = 78 flagstones. There are 2 flagstones left over. An additional truck is required. The correct answer is 4.
This problem reminds me of the questions on the Cognitive Reflection Test, featured in Thinking, Fast and Slow. The questions on that test are designed to have an answer which is “intuitive, appealing, but wrong”. Of course, LLMs are familiar with the original Cognitive Reflection Test questions, so it’s lucky for us that GSM8K (perhaps unintentionally) has a less-well-known question of the same style. It lets us see if LLMs fall for trick questions of this form, or if they’re able to notice when there’s more than meets the eye.
Grok 3 (Think) was the only prior model to get this question right reliably. When I tested using APIs, o4-mini-high got it right 0/10 times; Gemini 2.5 Pro got it right 3/10 times; and Grok 4 got it right 10/10 times. Grok 4 in the web app got it wrong something like half the time; I’m not sure what’s going on there. While this ability was already notable in Grok 3 (Think), I think it’s more notable now that Grok 4 has advanced to the frontier.
Grok 4 Heavy in the web app gets it right, though it tends to search the web.12 I would guess that it only needs one of its parallel instances to get the right answer in order to realize that the others are mistaken by comparison, so I would guess that it gets this right reliably even if disconnected from the web.
Grok 4 also usually gets a counterintuitive geometry problem
The next example was inspired by a children’s toy, pictured below.
Consider a tetrahedron, two of whose faces are equilateral triangles with unit side lengths, and two of whose faces are 45-45-90 right triangles with unit leg lengths. Glue two such tetrahedra together along the right triangle faces. Describe the resulting polyhedron.
The easiest way to solve this problem as a human is to make a physical model, at which point the answer becomes obvious: it’s a square-based pyramid. The two initial tetrahedra are what you get if you slice the pyramid with a vertical plane that passes through the top vertex and a pair of opposite base vertices, along the red tiles in the photo below.

This is counterintuitive because, in general, when you glue two tetrahedra together you get a shape with 6 faces: each tetrahedron has 4, so 8 in total, but you subtract the 2 faces that got glued together, leaving 6. In this case, however, it happens that 2 of those 6 faces line up in the same plane. Namely, two of the 45-45-90 triangles become the square base of the pyramid. The resulting shape, the square-based pyramid, has only 5 faces. Thus, a bit like the flagstones problem, there is a “default” answer that is wrong. For a human, physical perception is the easiest route to realizing this.
I like this problem because it helps us answer two questions. Do models realize that this case is exceptional? And, if so, do they do so by using anything we’d recognize as spatial intuition?
Accessed via API, Grok 4 gave the right description 6/10 times. The other 4/10 times it described the incorrect general case of a triangular bipyramid with 6 faces. Gemini 2.5 Pro got it right 3/10 times; o3 and o4-mini-high got it right 0/10 times.
As for the method, Grok 4 always uses coordinates. Even if that doesn’t show novel spatial intuition, it does reinforce what we found on the flagstones problem: we might say Grok 4 is “careful”. In both cases, it checks an initial guess thoroughly enough to, at least sometimes, realize that there’s more to the story.
I would again expect Grok 4 Heavy to do well here.
That said, Grok 4 can still make simple mistakes
I tried Grok 4 on the few other GSM8K questions that Grok 3 (Think) got wrong and found one case of a very straightforward error. This is shown below in its summarized chain of thought on the web UI.
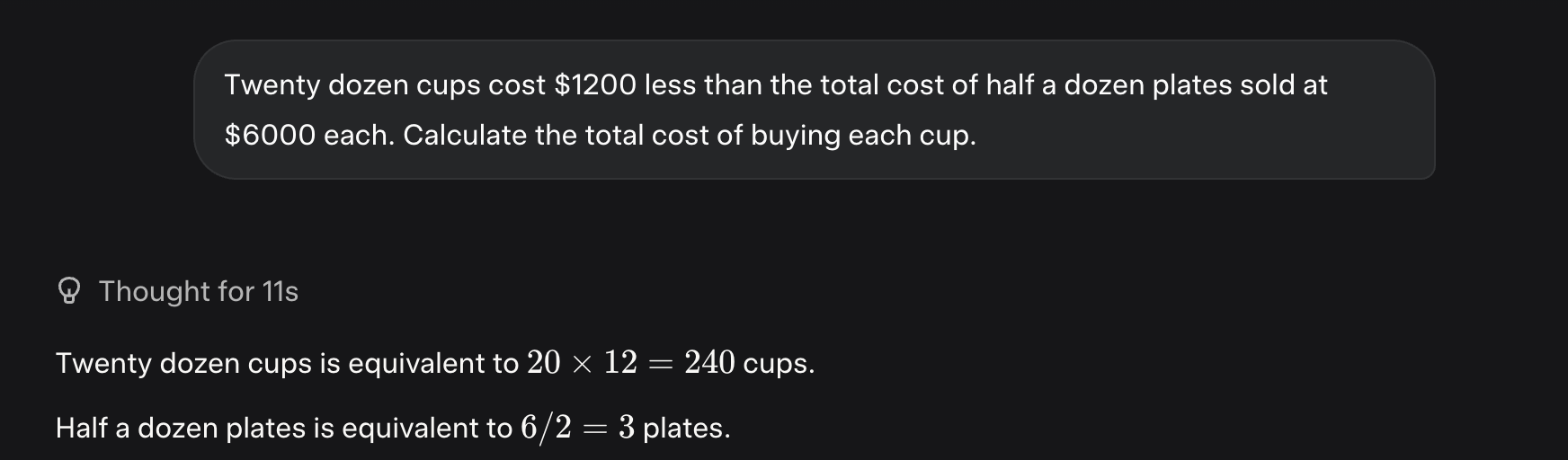
You’d think after just stating the meaning of “dozen” correctly on one line, it wouldn’t mess it up on the very next line, but no. To be clear, this sort of mistake isn’t at all unique to Grok 4. It’s also presumably quite rare, or it wouldn’t score as well as it does on benchmarks. But it does show that Grok 4 hasn’t completely solved the problem of basic reliability.
I tried this with standard Grok 4 via the API and it got the right answer 6/10 times. I would again guess that this means Grok 4 Heavy would get this right, even if not connected to the web.
Grok 4’s mathematical reasoning is not very human-like
We’ve seen plenty of evidence for this already, e.g. how it uses “grind it out” computations instead of more conceptual arguments. In this section I’ll just synthesize specific observations of this sort and offer a couple more examples.
Note that, as far as I have seen, this general conclusion is true of all LLMs today.
Grok 4 relies on Cartesian coordinates where humans would use spatial intuition
On various competition problems, as well as the tetrahedron-gluing problem above, Grok 4 preferred coordinate-based approaches to anything a human would recognize as higher-level geometric intuition.
To round out this geometric picture, I also looked at a simple instance, Problem 2 from the 2025 AIME:
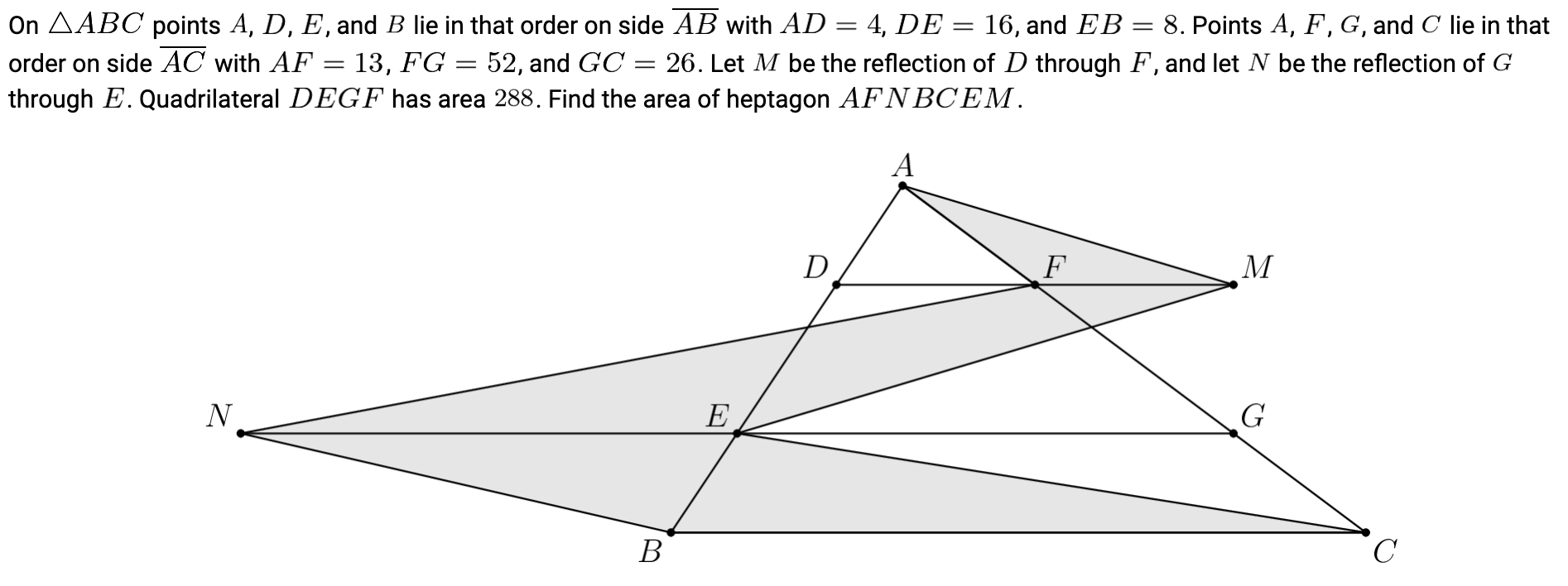
This problem takes a moment to understand, but it has a simple solution: the bottom chunk of the grey region is equal in area to the bottom chunk of the triangle. So too for the middle and top chunks. Thus, you can ignore the heptagon and just find the area of the triangle, which is easy to do using basic geometry theorems.
All frontier models get this right, but none, including Grok 4, solves the problem this way. Instead, they all use the given information to place the vertices of the shaded region in the xy-plane. They then use the shoelace formula, which lets you calculate the area of a polygon given the coordinates of its vertices. It’s a perfectly valid way to solve the problem, but it lacks any geometric insight.
For now, spatial intuition seems to be uniquely human.
Grok 4 doesn’t solve problems with off-the-beaten-path thinking
Again, we have seen several examples of this already, e.g. how some of its most impressive solutions relied heavily on background knowledge. I’ll add one more example now, a personal favorite. This problem is from the 2024 IMO. As far as I know, no solution to it relies on “grinding” or on background knowledge.
Turbo the snail plays a game on a board with 2024 rows and 2023 columns. There are hidden monsters in 2022 of the cells. Initially, Turbo does not know where any of the monsters are, but he knows that there is exactly one monster in each row except the first row and the last row, and that each column contains at most one monster.
Turbo makes a series of attempts to go from the first row to the last row. On each attempt, he chooses to start on any cell in the first row, then repeatedly moves to an adjacent cell sharing a common side. (He is allowed to return to a previously visited cell.) If he reaches a cell with a monster, his attempt ends and he is transported back to the first row to start a new attempt. The monsters do not move, and Turbo remembers whether or not each cell he has visited contains a monster. If he reaches any cell in the last row, his attempt ends and the game is over.
Determine the minimum value of n for which Turbo has a strategy that guarantees reaching the last row on the nth attempt or earlier, regardless of the locations of the monsters.
The top and bottom rows have no monsters. The other 2022 rows each have one monster. Since there are 2023 columns, “at most one monster per column” means there’s a single safe column and each other column has one monster. The question is, what’s the fewest number of attempts Turbo needs to get from (say) the top row to the bottom row?
2023 is sufficient: go straight down each column, and eventually you’ll find the safe one—though it might be the last one you try, if you get unlucky. Can you do better? With this sort of problem, either there’s a clever way to do better, or a clever way to prove that it’s impossible to do better. Playing around, there are some promising patterns. For instance, if you ever find two monsters in adjacent columns that are not in diagonally adjacent cells, then you can zigzag around them, as shown on the left below. But if the monsters are in diagonally adjacent cells, this doesn’t work, as shown on the right. In fact, the monsters could be in one big diagonal running across the whole grid, so the pattern on the left never appears. Of course, maybe there’s a strategy that would take advantage of this…
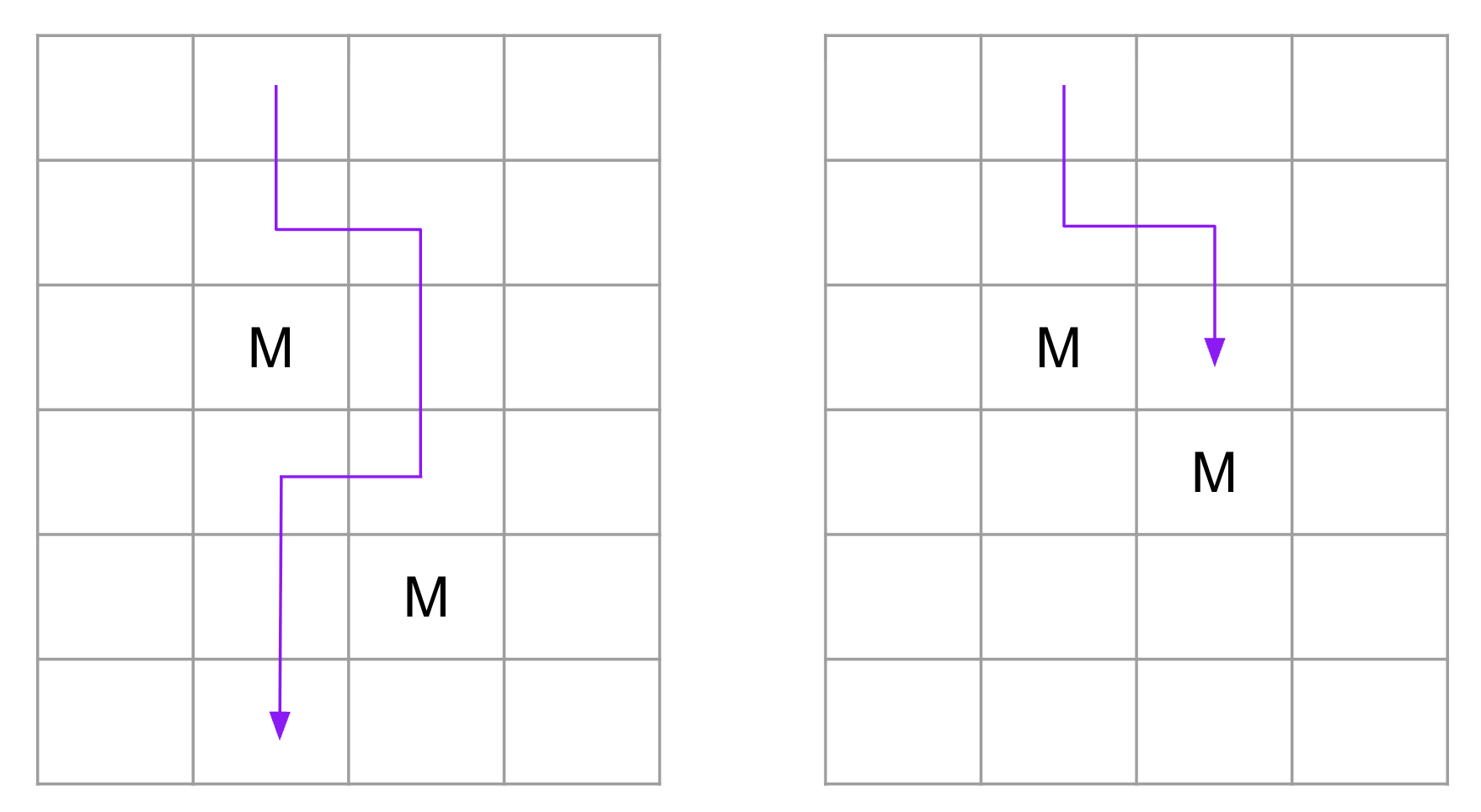
That’s just the start, but it shows the style of thinking you have to engage in. Also, the final answer is somewhat counterintuitive: only 3 attempts are needed to guarantee success, and this is the same for other, similar grids, e.g. with 1000 rows, 999 columns, and 998 monsters. The strategy is not easy to find and, subjectively, quite clever.13
Big picture, I like this problem because I think it requires some of the same skills I imagine bottleneck progress on harder research problems, even practical ones. If AI starts solving problems like this, I will personally expect to see more novel mathematical and scientific breakthroughs.
But, for now, no LLM has made any progress on this problem. Grok 4 got it wrong all 10 times I sampled via the API. Amusingly, it actually got the right final answer several times, but with a completely invalid strategy: it said to use two attempts to discover the locations of the monsters in two adjacent columns, and then zigzag between them on the third attempt. Of course, this won’t work if the two monsters happen to be diagonally adjacent to each other, as shown in the right half of the above diagram. Grok 4 didn’t seem to realize this.
Conclusion
Grok 4 has reached the frontier of AI math capabilities—an impressive feat for a company founded less than two years ago. I take it as evidence that, apart from capital, there is not a huge moat around LLM math capabilities.
What next? xAI reported that they trained Grok 4 with a great deal more reinforcement learning (RL) than their previous models. For their efforts, they got what I would say is a clear—but incremental—step forward. Returns have always been diminishing: exponential increases in input yield only linear gains in output. But, qualitatively, this drives home for me that scaling up today’s RL to frontier levels of compute doesn’t immediately deliver AI systems capable of doing a mathematician’s job. That will either take further scale, ostensibly quite a bit of it, or different methods.
Thanks to Jasper Dekoninck and Ivo Petrov for consultation on some of Grok 4’s outputs.
Notes
-
Note: they did not use Grok 4 Heavy. We chose to focus on Grok 4 given how unpredictably long it can take Grok 4 Heavy to return, opting for more interactions of perhaps not the very highest quality. Both mathematicians have extensive experience using other LLMs for math. ↩
-
In the case of the AIME and HMMT, xAI’s results are statistically indistinguishable from MathArena’s results. xAI didn’t report numbers for OTIS Mock AIME. ↩
-
There are two HMMTs each year, one in February and one in November. This is the February one. ↩
-
This is a subjective claim, but I base it on having reviewed dozens of solutions from multiple leading LLMs. See e.g. here and here. ↩
-
Why is this one unsolved? It’s typical of a harder AIME problem, requiring a bit of background knowledge and then a fairly lengthy case-by-case computation. Like the previous problem, it appears to be just a bit too much of a grind for current LLMs. I sampled Grok 4 by API on it 100 times, and it got the right answer twice. I would expect future models to get the answer right more reliably. ↩
-
This varies somewhat from year to year. For instance, the 2025 IMO was a bit of an outlier with more like 3 easy, 2 medium, and 1 hard. ↩
-
“Easy” here is relative! Most high school students could not solve any of these problems. ↩
-
Some model developers worked with the organizers of the 2025 IMO to have the same graders who graded human solutions also grade model solutions. That’s a step in the right direction, but I think it falls short. Most importantly, no grading rubrics or detailed solution evaluations have been published. This makes it difficult to apply uniform judgements to the solutions of other models, which is all the more relevant since it’s not clear whether this collaboration was open to all model developers. ↩
-
Google first announced a system called “Gemini 2.5 Pro Deep Think” in May. That’s the one I’m referencing here, which they internally graded as being state-of-the-art on the 2025 USAMO at the time. Then, in July, Google announced a system simply called “Gemini Deep Think” which won a gold medal on the 2025 IMO. Neither system is publicly available. ↩
-
Google did release a proof for this one medium problem, which I’ve written about here. ↩
-
This excludes FrontierMath runs conducted internally by OpenAI, e.g. results for ChatGPT agent discussed here. OpenAI has exclusive access to FrontierMath problems. ↩
-
Yes, even for simple word problems! ↩
-
This exposition is borrowed from here, where you can also find a link to the solution. ↩