We didn’t learn much from the IMO

Published

Aug 07, 2025

Authors

Resources

A few weeks ago I laid out what I thought the IMO might tell us about AI math capabilities. The IMO has now happened, with Google and OpenAI both announcing experimental LLMs that solved the same 5 of the IMO’s 6 problems—just enough for a gold medal. What did we learn?

There was understandably a lot of excitement about the gold medals, but I think a closer look shows that this achievement tells us little about capabilities progress. This is due to bad luck: the 5 solved problems happen to be no harder than problems AI systems could already solve, and the one unsolved problem was much harder than anything any system has solved.

I’ll use this post to make the case that we didn’t learn much from the IMO. I’ll take both an “outside” view, using statistics about the problems and the performance of prior AI systems, and an “inside” view, taking a closer look at the specific problems and the AI solutions.

Viewed from outside, the sample of problems looks uninformative

The main issue is the difficulty distribution of this year’s problems: it was unusually lopsided. This becomes clear to see if we plot the MOHS difficulty ratings as judged by US IMO team coach Evan Chen.

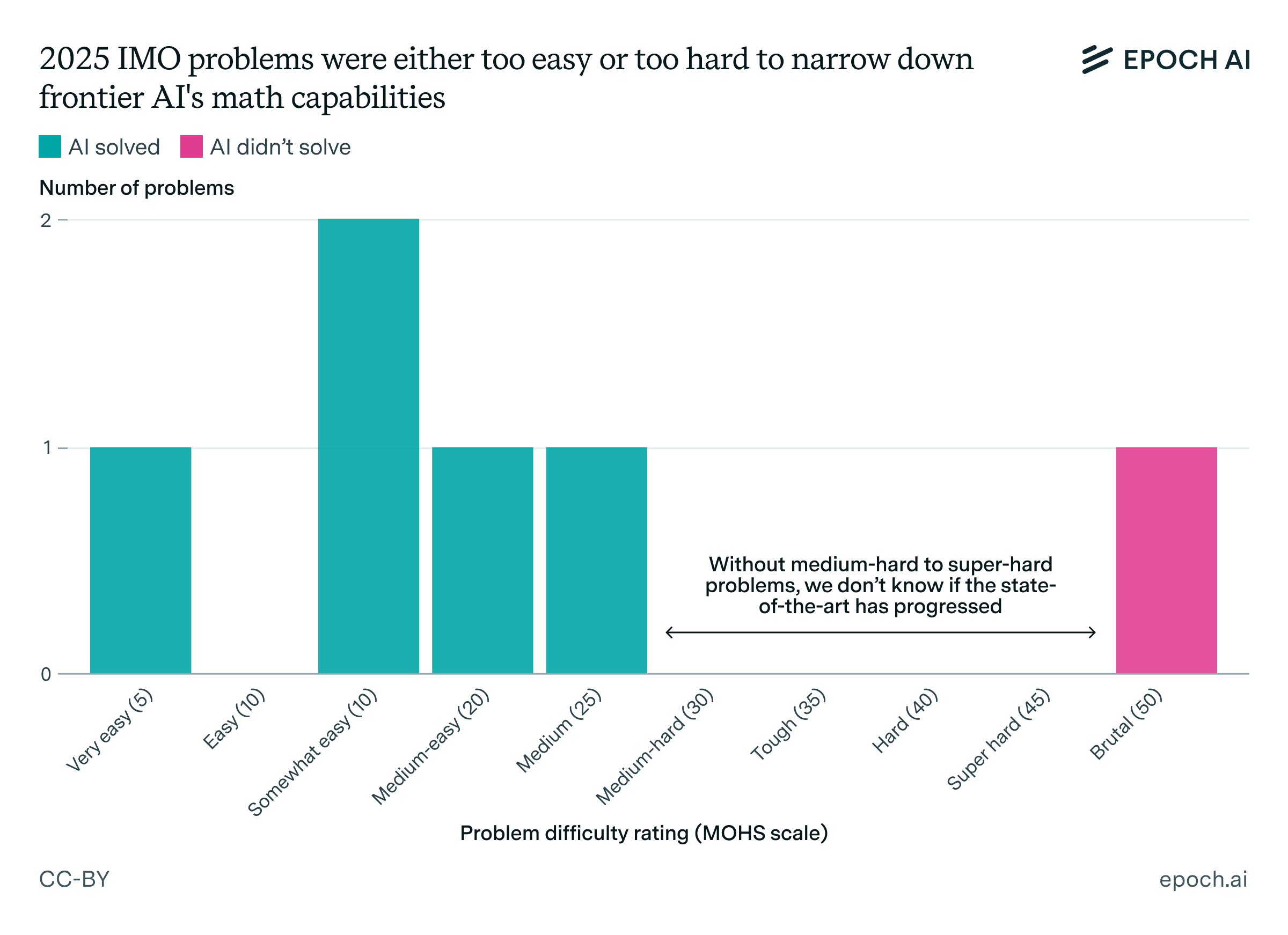
The IMO usually has two easy, two medium, and two hard problems, according both to general perception and Chen’s more granular data.¹ 2025 was unusual in that it only had one hard problem. Since 2000, which is when Chen’s data begins, there has only been one other time when ≥5 problems had MOHS ≤25. Worse, the one hard problem this year was very hard: according to Chen, there have only been two other such “brutal” (MOHS 50) problems on the IMO since 2000.²

Taken at face value, this means AI math capabilities are somewhere between “medium” and “brutal”. I’ll argue that solving these easy-to-medium problems represents only incremental progress: a step forward primarily in terms of reliability, but not a sign of the emergence of any new capability. By the same token, failing to solve the “brutal” problem only rules out extremely rapid progress. That’s not to say these new models don’t have any new capabilities, just that we can’t tell it from this year’s IMO.

AI systems were already performing at this level

If you didn’t know that AI systems could solve easy-to-medium problems on elite high school math competitions, then this gold medal result should certainly update your understanding. But a close look at the performance of various AI systems from the past year suggests that this capability is nothing new.

Prior to the IMO, Deep Think had already solved a “medium-hard” problem, and older models seemed close to doing so

In May, Google announced that Gemini 2.5 Pro Deep Think had solved a MOHS 30 problem (“medium-hard”) on the 2025 USAMO³. I wrote in the previous article that this problem required careful application of background knowledge and some depth, but nothing particularly off-the-beaten path. In other words, we already knew that there was a style of medium-difficulty IMO problem within reach for Deep Think. Solving the 2025 IMO problems in the MOHS 5-25 range doesn’t immediately suggest anything more impressive than this.

To be fair, that could just mean that Deep Think was impressive back in May! But even the USAMO performance wasn’t a surprise. In March of this year, when the USAMO took place, no model did well at first. But I wrote at the time that available models like o3-mini seemed to have a lot of the necessary raw material for solving many of these problems, including the very MOHS 30 USAMO problem which Deep Think went on to solve, and that minor improvements could probably get them there. So, I see Deep Think’s performance on the USAMO and IMO as simply realizing this latent potential.

Some currently-available models did decently on the IMO

MathArena evaluated models that were released prior to the IMO on the IMO problems. The results weren’t half bad. The top scorer was Gemini 2.5 Pro: in a best-of-4 setting it solved the MOHS 25 problem and got significant partial credit on the two MOHS 15 problems. On these latter two problems, MathArena noted that the gap to full credit didn’t seem too severe, suggesting “that models could improve significantly in the near future if these relatively minor logical issues are addressed.”

It’s a bit novel that currently-available models can sometimes solve medium-difficulty IMO problems: we hadn’t seen this so clearly on uncontaminated problems. But this raises the floor for what the experimental models would have to do to demonstrate incremental progress: given that they didn’t solve the hardest problem, there’s not much room left.⁴

We can’t even conclude that LLMs caught up to AlphaProof

In my previous article I noted it would be interesting to see whether LLMs could match the performance of the previous AI IMO record-holder: Google’s specialized AlphaProof system, which solved 4/6 problems on the 2024 IMO. In particular, AlphaProof’s most notable achievement was solving a “hard” MOHS 40 problem. Its solution wasn’t very insightful, but the fact that it managed a proof at all was interesting.

Again, the difficulty distribution worked against us here: the 5 solved problems on this year’s IMO were all significantly easier, and the one hard problem was significantly harder, than the hardest problem that AlphaProof solved.⁵ The experimental LLMs didn’t get the chance to compete directly.

An inside view confirms that these easy-to-medium problems didn’t require new capabilities

What are these problems actually like? Do we see anything surprising in the experimental systems’ proofs? In particular, I was hoping for some problems that would require what humans recognize as creativity or conceptual thinking—but weren’t that hard by human standards. Alas, I don’t think any of the easier 5 problems require anything that existing models haven’t demonstrated: they all have a bit of a “just do what’s obvious” style.⁶ The one hard problem, on the other hand, requires just about every skill any IMO problem ever does, all at once.

Here’s a brief summary of my assessment of the problems and AI solutions.⁷

Problem (MOHS)	Domain	Human perspective	How AI did
1 (5)	Combinatorics / Geometry	Pretty easy: a single insight cracks it.	Struggled with the geometric aspect, but managed to overcome this with lots of algebra.
2 (20)	Geometry	Total grind: not a very interesting problem.	Grinded through it.
3 (25)	Number Theory	Surprisingly straightforward: "do the obvious thing" works.	Solutions follow the straightforward approach that humans also take.
4 (15)	Number Theory	Straightforward: a fair amount of case-by-case analysis.	Solutions follow the straightforward approach that humans also take.
5 (15)	Algebra	Straightforward: "do the obvious thing" works.	Solutions follow the straightforward approach that humans also take.
6 (50)	Combinatorics	Very hard. Requires creativity and abstraction. Solutions are long.	Couldn't get the right final answer, let alone a proof.

I’ll give a few examples from the problems I found most notable.

Funnily enough, the first problem might be the most interesting, even though it’s the easiest for humans. It’s a combinatorics problem with a geometric flavor, which LLMs have tended to struggle with due to their general lack of spatial intuition. No publicly available model solved it on MathArena. How did the experimental models solve it? Here’s the problem:

The figure below shows such a configuration for n=4, with one sunny line.

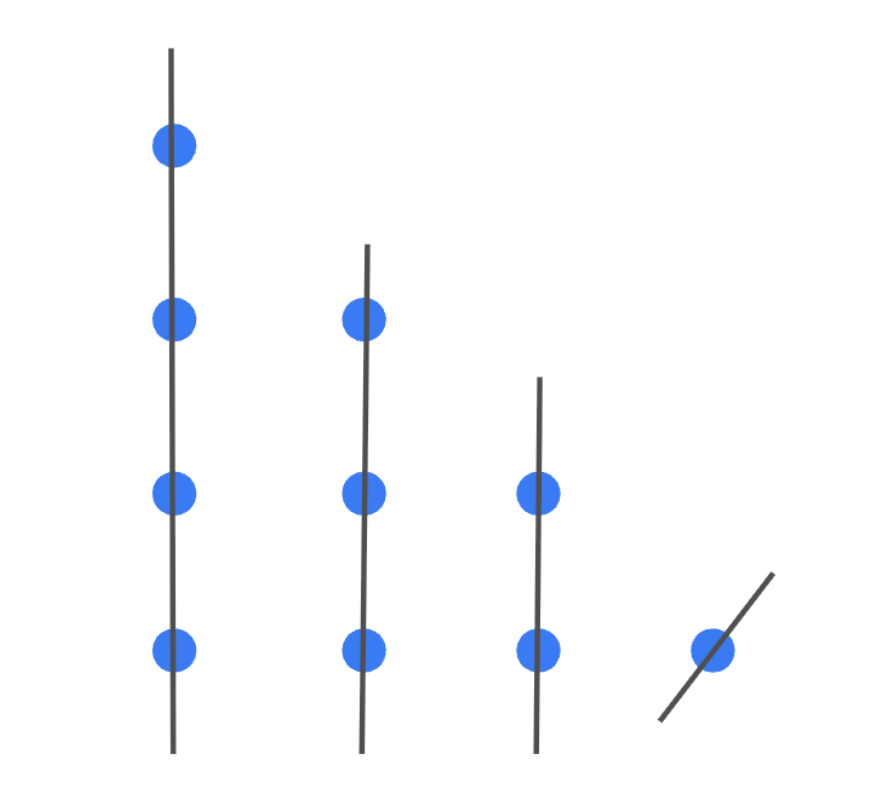
The key observation for a human is that, when n≥4, one of the lines must cover one of the sides of the triangle. Once you realize that, you can reduce the problem to simply analyzing the n=3 case. Here’s how Chen’s reference solution expresses this reduction:

Hence, by induction we may repeatedly delete a [side] line without changing the number of sunny lines until n = 3 (and vice-versa: given a construction for smaller n we can increase n by one and add a [side] line).

LLMs seem to struggle with this step. They do prove it, but rather than a one-sentence argument like Chen’s, they use paragraphs of algebra. Here’s Google’s solution, and OpenAI’s is logically similar:

I think what’s going on here is that the LLMs cannot use anything like human spatial intuition to see that removing or adding a side line results in a similar triangle, so they have to use a more symbolic approach to reach the same conclusion. I’ve observed this lack of spatial intuition before with LLMs, most recently in an analysis of Grok 4’s math capabilities but also previously on my personal blog. I would guess that the LLMs just needed more “thinking time” to find this algebraic workaround.

How about the hardest-for-humans problem that the AI systems solved? Here it is.

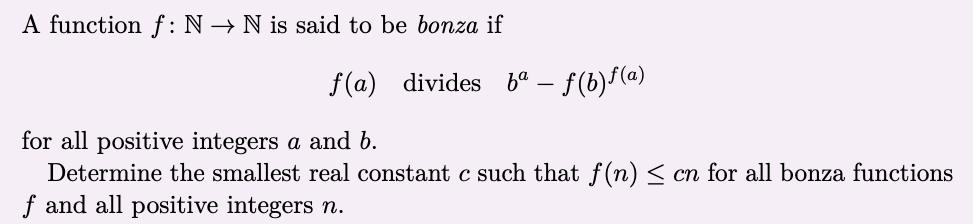
Unfortunately, this problem cracks if you “just do what’s obvious”, and LLMs have been good at that for a while. One math YouTuber had this to say about the problem:

Typically in my videos I will actually have a “motivation” section. But, in this case, this problem is actually quite straightforward in the sense that, as you motivate yourself to investigate it, you actually end up with the solution.

In this problem, the given divisibility condition is highly productive: since it holds for all positive integers a and b, you can plug in different values for a and b and get a lot of information. Furthermore, since the given property is about divisibility of integers, you might naturally try plugging in some prime numbers, and that cracks the whole thing.

Here is an outline of Chen’s reference solution:

f(n) divides nⁿ for all n.
Either f(n)=n or f(p)=1 for all odd primes p.
f(n) is a power of 2 for all n.
f(n) is less than 4 times the highest power of 2 that divides n, i.e. f(n)≤4n.
Construct an example where f(n)=4n for some n.

The proofs from the experimental LLMs follow this path, with minor variations. For example, here is OpenAI’s proof of part of the third step outlined above.

4. Structure in non-identity case.

First, show no odd prime can divide any value.

Suppose n with odd prime r | f(n). Obs O: f(n)|n^n -> r|n. Now P_f(n,r): modulus f(n) divisible by r.
So r | r^n - f(r)^{f(n)}. But f(r)=1 (r odd). So need r| r^n - 1. r^n divisible by r, difference -1 mod r, impossible. So cannot. So indeed:

(**) In non-identity case: for all n, f(n) has no odd prime factors. So f(n) is power of 2 always.

Incidentally, you’ll notice that the model’s linguistic style is oddly telegraphic: perhaps more like a raw chain-of-thought than final output. I don’t know the reason for this, but suspect it’s not too significant: the logic is perfectly human-like, even if the phrasing is unusual.

Finally, I’ll mention that the hard problem was really hard. It’s quite easy to understand, though.

You can do a lot better than the naive guess of 4048, but even finding the right answer is hard: no LLM did so.⁸ Then, proving that this non-obvious answer is in fact best-possible is another matter entirely. I’d previously characterized hard IMO problems as requiring abstraction, creativity, and depth: abstraction meaning the need to derive general truths, creativity meaning the need to come up with something new, and depth meaning the number of steps required to carry out a solution. This problem requires a lot of all three. It would have been more informative to get a moderately easier problem with this same overall character.

The IMO was at least an interesting case study in reliability on hard-to-verify domains

Doesn’t a gold medal count for something? I do think there’s a real accomplishment here, but it has more to do with reliability. Namely, the experimental models were only allowed a single submission, and they managed to solve these five problems anyway, without a single logical gap.

This is all the more interesting because natural-language proofs are in a sweet spot where automatic verification isn’t possible, but humans have very well-developed criteria for what makes a proof valid. Can LLMs be made to understand such criteria with high precision? This is relevant far beyond math, touching on any domain where outputs are hard to verify but where humans generally “know it when they see it”.

If nothing else, the IMO showed that cranked-up LLMs can indeed deliver reliable results in one such domain, at least when the required reasoning isn’t too hard. But, in terms of identifying the emergence of reasoning capabilities beyond medium-difficulty IMO problems, we’ll have to look to other evaluations.

Notes

For a sense of general perception, see, e.g., here. Of course “easy” is relative: most high school students could not solve even an easier IMO problem. ↩
I’ll rely heavily on the MOHS ratings for the “outside” view. They’re certainly subjective, but Chen is highly respected in the olympiad world, and this is as close to an authoritative expert opinion as we can get. ↩
The USAMO is a US national competition with the same format as the IMO and comparable difficulty. ↩
Note that for each of these 4 samples MathArena used a best-of-32 scaffold where the LLM judges its own solutions in a single-elimination bracket. That’s 1-2 OOMs of test-time compute scaling, and, anecdotally, they say this significantly increased performance. So, this isn’t quite “out of the box” performance, but it suggests that plain old test-time scaling gets much of the way to gold. In fact, a professor at UCLA has claimed to have elicited the full gold medal performance from Gemini 2.5 Pro only with a scaffolding, no additional training whatsoever. That result isn’t preregistered or independently verified, but I think it points in the same direction as everything else. ↩
This is too bad for AI company Harmonic, whose model generates formal proofs just like AlphaProof did and which solved the easier 5 problems on the 2025 IMO: they can’t claim to hav solved any uncontaminated IMO problems harder than what AlphaProof solved. ↩
You might be able to infer that from the MOHS ratings alone: my favorite IMO problem, which AlphaProof failed to solve, which all publicly available models fail to solve, and which I think requires something like creativity, was already MOHS 35. Even the currently publicly-available version of Deep Think got this one wrong each of the 6 times I sampled it, though this isn’t the version that won gold on the IMO. ↩
A researcher from OpenAI claimed that their model did at least know that it didn’t know the right answer to P6. This is plausible, as LLMs are decent judges of correctness of solutions to proof-based competition problems. ↩
I’m inferring this from the facts that (a) no AI system got partial credit on this problem, and (b) MathArena’s rubric awards 1 point for finding a construction that achieves the right final answer. ↩

About the authors

Greg Burnham is a researcher at Epoch AI. Prior to this, he worked at Elemental Cognition and Bridgewater Associates. He has a BA in mathematics from Princeton University.