Training compute growth is driven by larger clusters, longer training, and better hardware
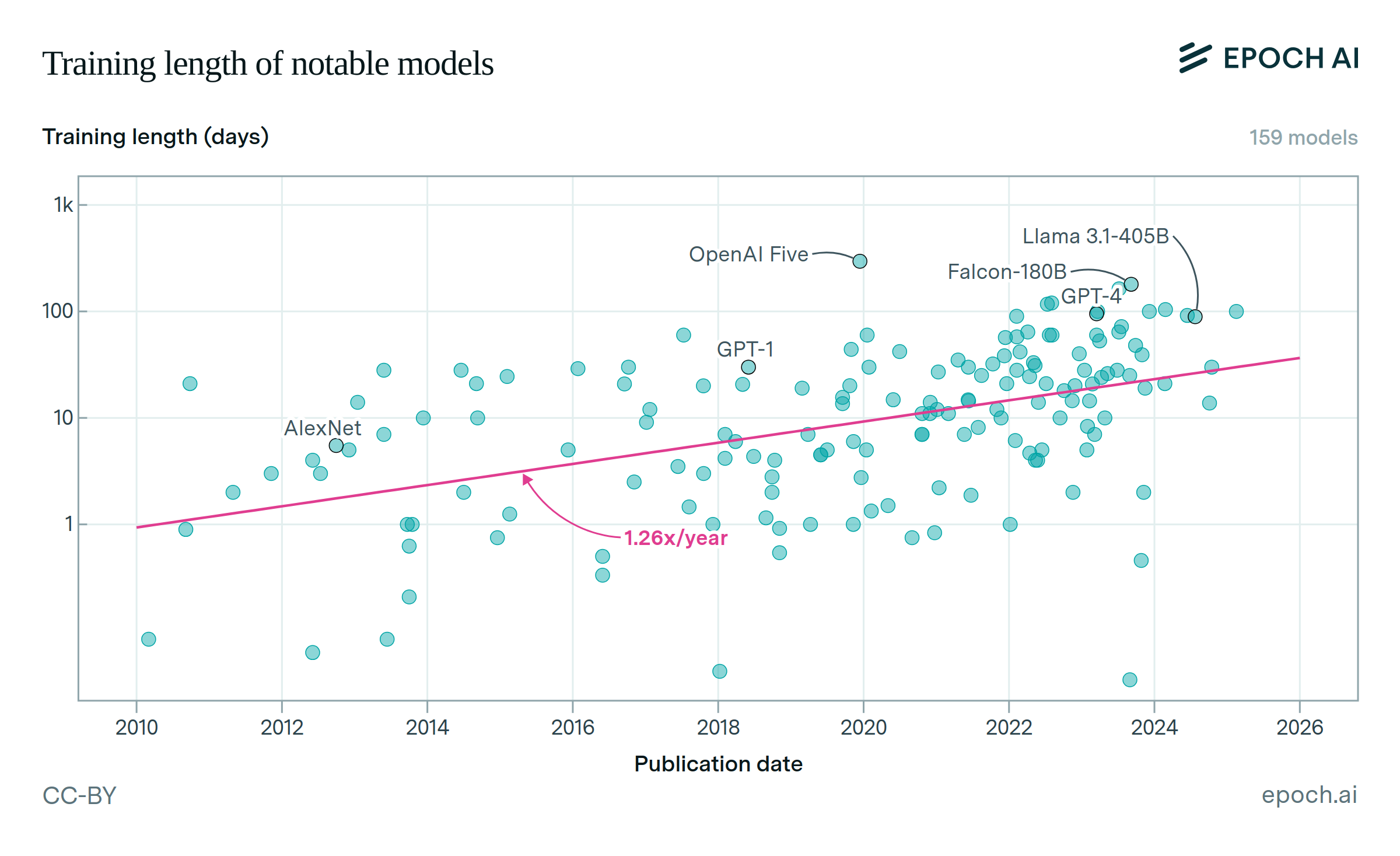
Since 2018, the most significant driver of compute scaling across frontier models has likely been an increase in the quantity of hardware used in training clusters. Also important have been a shift towards longer training runs, and increases in hardware performance.

These trends are closely linked to a massive surge in investment. AI development budgets have been expanding by around 2-3x per year, enabling vast training and inference clusters and ever-larger models.
Authors
Published
January 8, 2025
Learn more
Overview
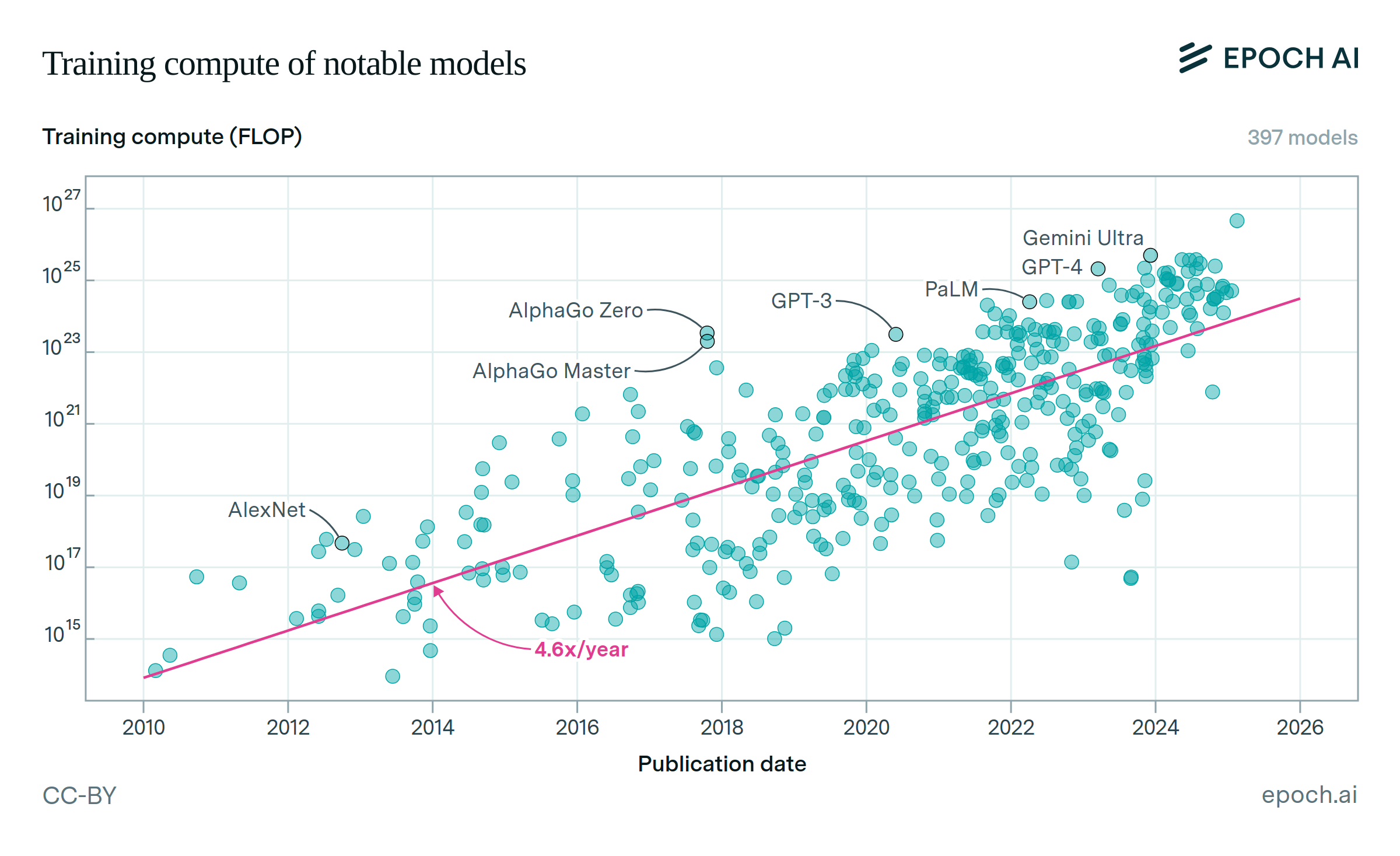
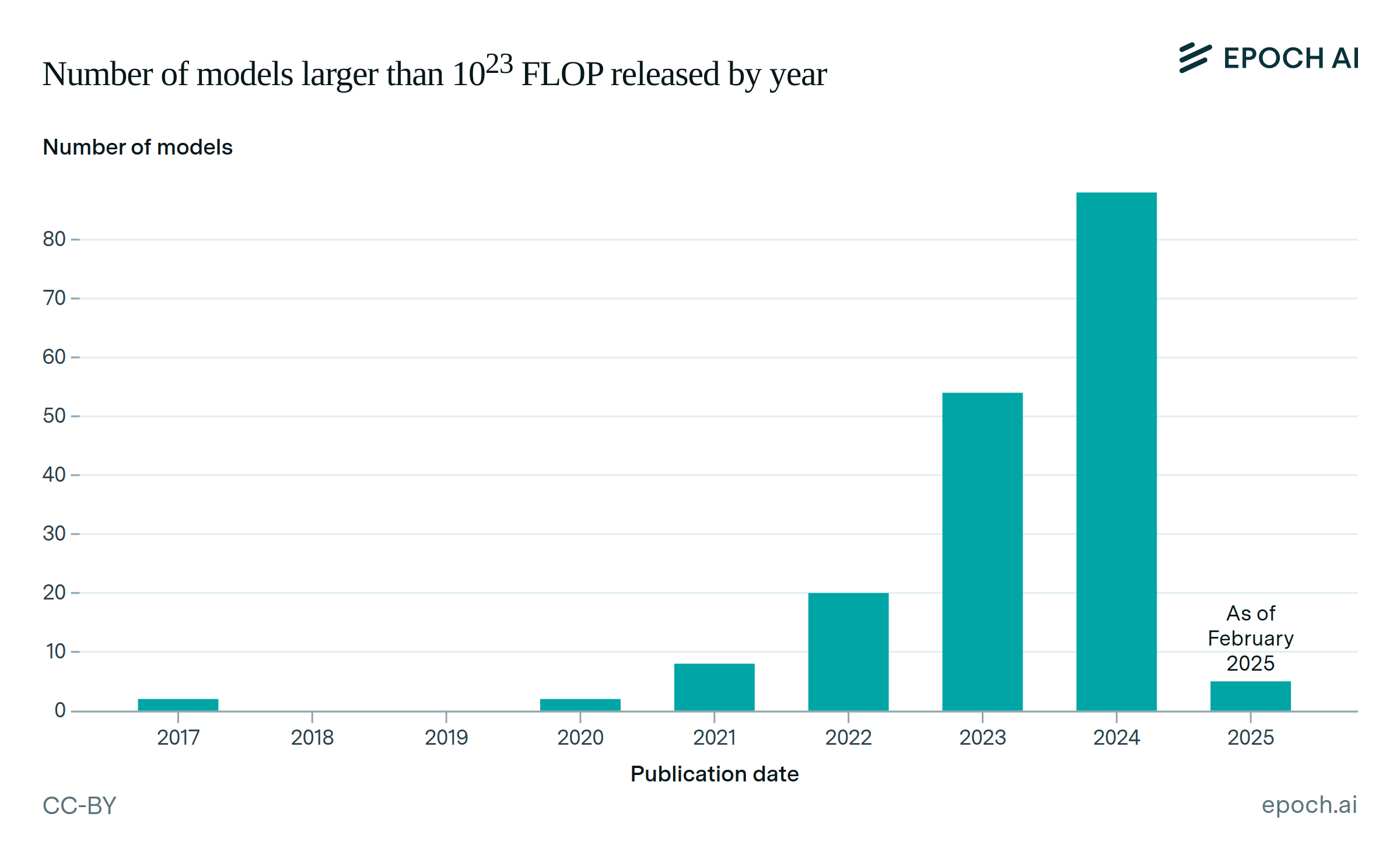
As training compute for frontier AI models grows rapidly, understanding the key drivers of this growth becomes increasingly important. We analyze three main factors: hardware cluster sizes, per-unit hardware computing power, and training duration. By fitting exponential trends to these factors, we calculate their relative multiplicative contributions to the overall growth in training compute. Our analysis focuses on frontier models developed after 2018—a period during which we previously observed a 4-5x growth rate in training compute. We also examined potential trends in hardware utilization rates, finding weak evidence of a positive trend. However, since the data quality is poor and their impact is small, we omit them from our main analysis.
Data
Our data come from Epoch’s Notable Models dataset, which includes data on the quantity and type of hardware used to train models, and training run duration.
In order to focus our analysis on recent frontier AI models, we filter our data as follows:
- Drop models that are fine-tuned from a base model.
- Of the remaining models, drop those that were not in the top 10 by training compute at the time of their release.
- Drop models published before 2018.
We refer to the remaining 63 models as frontier models after 2018. Note that models fine-tuned from base models are excluded in order to simplify analysis, since these are less reflective of trends in pre-training scaling.
To estimate a trend in hardware computing power (measured in floating-point operations per second, or FLOP/s), we additionally filter down to models where the training hardware is known. Hardware FLOP/s depends on the numeric format used during training, so we use the corresponding FLOP/s rate when the numeric format is known, and otherwise impute the most likely training format. The imputation procedure follows our usual decision procedure when estimating training compute via hardware details:
- If arithmetic precision is known based on details in the paper or associated code, use the hardware’s theoretical FLOP/s for that precision.
- Otherwise, use FP/BF16 tensor core performance if the training hardware used is able to benefit from it.
- Otherwise, if the hardware benefits from training at FP16 (without tensor cores), and the model was published after June 22, 2017 (the release of the V100 and a software update to the P100 enabling FP16 training), then use FP16.
- Otherwise, use the hardware’s FP32 FLOP/s value.
Note that we never assume the use of TF32, as FP/BF16 tensor core performance is better for all hardware models in our dataset.
Finally, when estimating trends for hardware FLOP/s and hardware quantity, we drop models with more than one linked hardware type, since in these cases we do not have unique values for these fields. For instance, some models are pre-trained on one type of hardware, and fine-tuned on another. This filter eliminates only 2 models from our analysis.
Analysis
We fit log-linear models against time for each of hardware FLOP/s, hardware quantity and training time. We bootstrap with replacement over our models to estimate confidence intervals (n=500). Our results are as follows:
| Variable | 10th percentile | Median | 90th percentile |
| Hardware FLOP/s | 1.36 | 1.41 | 1.48 |
| Hardware quantity | 1.5 | 1.69 | 1.91 |
| Training time | 1.37 | 1.53 | 1.71 |
| Combined product* | 3.58 | 4.27 | 4.93 |
| Training compute | 3.74 | 4.17 | 4.62 |
The product of the individual slopes is somewhat lower than the overall compute trend; this is the result of different missingness in each variable. However, we find that the combined product trend aligns well with a direct estimate of the trend on recorded training compute. We statistically test the difference between the two slopes across bootstraps, finding no statistically significant difference (90% CI: -0.4 to 0.7).
After obtaining estimates of slopes for each component, we calculate the multiplicative contributions of each trend to compute scaling as the logarithm of each trend’s slope divided by the sum of the logarithms of all slopes. This is done for each bootstrap sample, producing the percentages shown in the plot.
In addition to the three main factors identified above, we consider hardware utilization as a potential fourth category. Only a small subset of our models have hardware utilization estimates (n=22); among these models there is a slight positive trend of 1.1x per year (90% CI: 1.0 - 1.2). As a factor driving growth, this would be 7% (90% CI: 0% - 12%). Due to the small sample size and magnitude of the trend, we omit potential contributions from hardware utilization for the purpose of this analysis.
We next run a sensitivity analysis, perturbing N in our selection of the top N models. We find that estimates of the slope of training compute scaling, as well as the slopes and relative contributions from each underlying trend remain relatively stable for N = {5, 10, 15}, with no statistically significant differences. The most notable differences come in the top-5 model subset, where hardware quantity appears to have a relatively larger contribution compared to the top-10 subset (median: 0.48 vs 0.40).
Finally, we test the impact of different choices of year to begin our analysis. Overall, results are highly similar when using initial years between 2017-2019; the most significant change is that FLOP/s grows somewhat faster in the 2017-present data (1.6x per year, vs. 1.4x from 2018 on).
Code for all analysis is available at this Colab notebook.
Assumptions
We assume that exponential fits against time are a reasonable functional form for trends in hardware FLOP/s, hardware quantity, and training time. This assumption is more questionable for hardware FLOP/s, which shows a pattern of discrete steps between different generations of leading AI hardware. As a robustness check, we additionally fit a piecewise-constant model for hardware FLOP/s, and find that the distribution of annualized growth between the start and end point is not significantly different from the slope of a simple exponential fit (p-value: 0.79).