LLMs have not yet solved the hardest problems on high school math contests
A year ago, LLMs could only solve some of the easier problems on premier high school math contests. Now they have achieved gold-medal equivalent scores on the International Math Olympiad (IMO), the pinnacle of such contests. However, no LLM has solved even a single problem from the highest tier of difficulty on these contests.

Small sample size at this highest tier leaves uncertainty about LLMs’ precise capabilities here, but complete saturation is unlikely.
Authors
Published
September 3, 2025
Learn more
Overview
We construct a unified problem difficulty scale by combining the Art of Problem Solving’s competition ratings and US IMO coach Evan Chen’s Math Olympiad Hardness Scale (MOHS). We source accuracy data from MathArena for the AIME, USAMO, and IMO, and plot models that were state-of-the-art at the time of their release. We also plot the scores announced for the unreleased models that achieved gold-medal equivalent scores at the IMO.
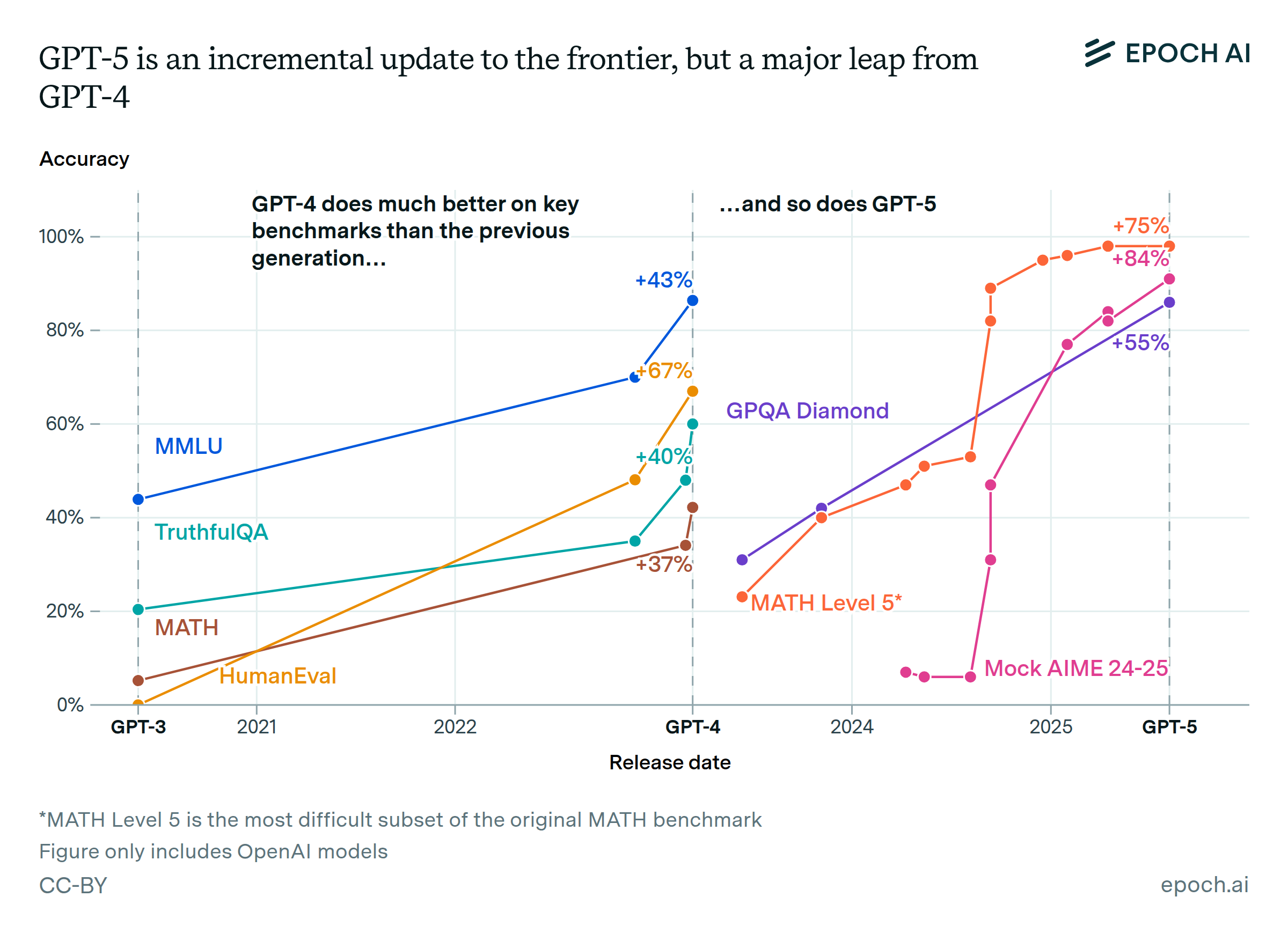
Publicly available models achieve >95% on problems up to a rating of 5. These models have not fully saturated problems rated 6-7, though GPT-5 achieves >67%. The remaining gap is due to reliability, i.e., it solves each problem at least once when sampled four times. The 2025 IMO contained three problems rated 7, two rated 8, and one rated 9. Certain experimental LLMs, e.g. Google’s Deep Think, solved all but the last of these. Since this sample size is small, we also test the publicly available Deep Think model on two easily-checkable 2024 IMO problems, rated 8 and 9, and find that it fails to solve each even a single time out of 10 samples.
Data
For competitions, we use the AIME, USAMO, and IMO. The first two of these are the premier high school math competitions in the US, and the third is the premier global competition; they are all professionally organized. We consider data only from 2025 to minimize concerns of contamination. Data is primarily sourced from MathArena, which evaluates models using a consistent elicitation and scoring methodology. Additionally, to reflect gold-medal performance achieved by several models on the 2025 IMO, we include Google’s Deep Think model, which tied for top performance among AI systems entered in the competition.
We use two sources for problem difficulty ratings. The first is a broad set of competition ratings which places problems from different competitions on a unified 10-point scale. This comes from the Art of Problem Solving (AoPS), a high school math enrichment and competition preparation company. The second is the Math Olympiad Hardness Scale (MOHS), a finer-grained scale focusing only on the highest tiers of problem difficulty, created and maintained by US IMO team coach Evan Chen. Whereas the AoPS scale only applies at the contest level, Chen assigns MOHS ratings to individual problems in the USAMO and IMO each year.
o1-mini was state-of-the-art on the AIME competition at the time of its release, but was not included in MathArena’s evaluations. We ran MathArena’s evaluation scaffold to augment the dataset with this additional model.
Data for this analysis can be found here.
Analysis
We categorize problems as follows:
| Difficulty Rating | Competition Problems |
|---|---|
| 2 | AIME 1-3 |
| 3 | AIME 4-6 |
| 4 | AIME 7-10 |
| 5 | AIME 11-13 |
| 6 | AIME 14-15 |
| 7 | USAMO/IMO MOHS 5-15 |
| 8 | USAMO/IMO MOHS 20-35 |
| 9 | USAMO/IMO MOHS 40-50 |
This deviates slightly from the AoPS scale at the lower end: they characterize 2 as “easiest AIME 1-3” and have a special 2.5 rating for “usual AIME 1-3”. We collapse this into the same rating, labeled 2, for ease of interpretation.
We use MOHS ratings to achieve finer-grained classification in the 7, 8, and 9 buckets. This is highly consistent with the AoPS descriptions. For instance, it characterizes “easiest USAMO and IMO 3/6” as 8s, whereas “average USAMO and IMO 3/6” are 9s. We thus group the 10 ratings of the MOHS scale into sets consisting of {5, 10, 15}, {20, 25, 30, 35}, and {40, 45, 50} and assign those overall ratings of 7, 8, and 9.
We omit the 1 and 10 ratings. The former corresponds to “traditional middle/high school word problems” and no actively-evaluated competitions cover this difficulty level. The latter corresponds to “historically hard problems, generally unsuitable for very hard competitions”.
We include models in the main diagram according to whether they score over 5% higher at any difficulty rating, compared to all previously-released models in the dataset. Models are ordered left-to-right by their release date.
We now discuss the degree of saturation at each level.
Difficulty 2-5. These problems pose little remaining challenge: multiple models now score above 95% in each rating.
Difficulty 6. GPT-5’s 69% is the top score at this rating. The gap to 100% reflects a lack of reliability as opposed to a lack of capability: GPT-5 (high) solves each problem at least 1/4 times on MathArena.
The sample size at this rating is small, with only four AIME problems included. To augment this, we also look at a student-organized competition, HMMT, that is also evaluated by MathArena. The AoPS scale rates the more difficult half of HMMT, consisting of 15 problems, as 5.5-6. GPT-5 (high) scored 78% on these, solving all but one problem at least once; other models, including GPT-5-mini (high), solved that one unsolved problem at least once.
Difficulty 7. The situation is similar: not completely saturated, but each of the five problems evaluated by MathArena has been solved at least once. Furthermore, the IMO Gold models all solved the three 7-rated problems on the 2025 IMO in their one-and-only attempt, suggesting that the experimental techniques used by those models can close this reliability gap.
Difficulty 8. The dataset contains four problems with difficulty 8: two each from the 2025 USAMO and 2025 IMO. While MathArena stopped grading 2025 USAMO solutions in June, xAI subsequently reported an internal run of Grok 4 Heavy to have solved the two problems from the USAMO. All of the IMO Gold models solved the two problems on the IMO. Thus, the available data suggests that problems at this rating may be nearly saturated.
Difficulty 9. The dataset contains two problems rated 9, one each from the 2025 USAMO and 2025 IMO. No model has solved either one even once, though there are no publicly available results from the IMO Gold models on the USAMO problems.
To augment this small sample, we test the publicly available version of Deep Think on the two easy-to-check problems from the 2024 IMO: P5 which is rated 8, and P6 which is rated 9. This version of Deep Think is “a variation” of the IMO Gold model, though Google reports that it does somewhat worse on the IMO problems (61% vs. 83%). We thus sample it 10 times for each problem to compensate for this lower baseline performance. It does not solve either problem in any sample.
On the 2025 USAMO problem rated a 9, MathArena awarded o3-mini (high) 0.5 points of partial credit, out of a total of 7. This corresponded to a largely incomplete solution which started in generally the right direction. We don’t consider this to be meaningful progress toward solving the problem.
Assumptions
As discussed above, our main limitation is sample size. Even with our modest augmentation, we only have three problems with difficulty rating 9. In concluding that the flat score of zero represents non-saturation at this rating, we are assuming that these three problems are not extremely idiosyncratic.