If you’re reading this, you’ll no doubt have heard of the impressive progress that state-of-the-art language models have been able to make in solving math problems. For instance, we recently found that o4-mini outperformed the average team of mathematicians in our human baseline competition.

However, these numbers alone provide limited insight into what exactly these models are or aren’t able to do, and why. How do reasoning models solve complex math problems? Do they reason similarly to human mathematicians? And where do they fall short?

To answer these questions, we asked fourteen mathematicians to analyze 29 of o3-mini-high’s raw, unsummarized reasoning traces on FrontierMath problems, which OpenAI shared with us.¹ Our goal in this post is to share the main takeaways from this survey, and discuss what this means for future developments at the intersection of AI and math.

Stay one step ahead

Get the latest from Gradient Updates in your inbox

Subscribe

How does o3-mini-high solve FrontierMath problems?

Extreme erudition – and it’s not just memorization

Out of the 29 reasoning traces, 13 of them resulted in a correct response – but how does o3-mini-high solve these problems?

One important factor is its extreme erudition, and this should come as no surprise given how much data it’s been trained on. The model is able to tackle FrontierMath problems across a wide range of domains, and the mathematicians unanimously agreed that it is extremely knowledgeable. One mathematician noted that “[o3-mini-high] correctly expands the mathematical background of the question, involving very fancy concepts […] - general knowledge and understanding of the question are not the bottlenecks here.”

And it’s not pure memorization either. Even when the required techniques for solving a problem were deliberately obscured by question authors, the mathematicians generally found that o3-mini-high has a decent ability to draw on the right theorems to make progress. In particular, on around 66% of the reasoning traces, the mathematicians rated the model at least 3 out of 5 for its ability to invoke relevant mathematical results.

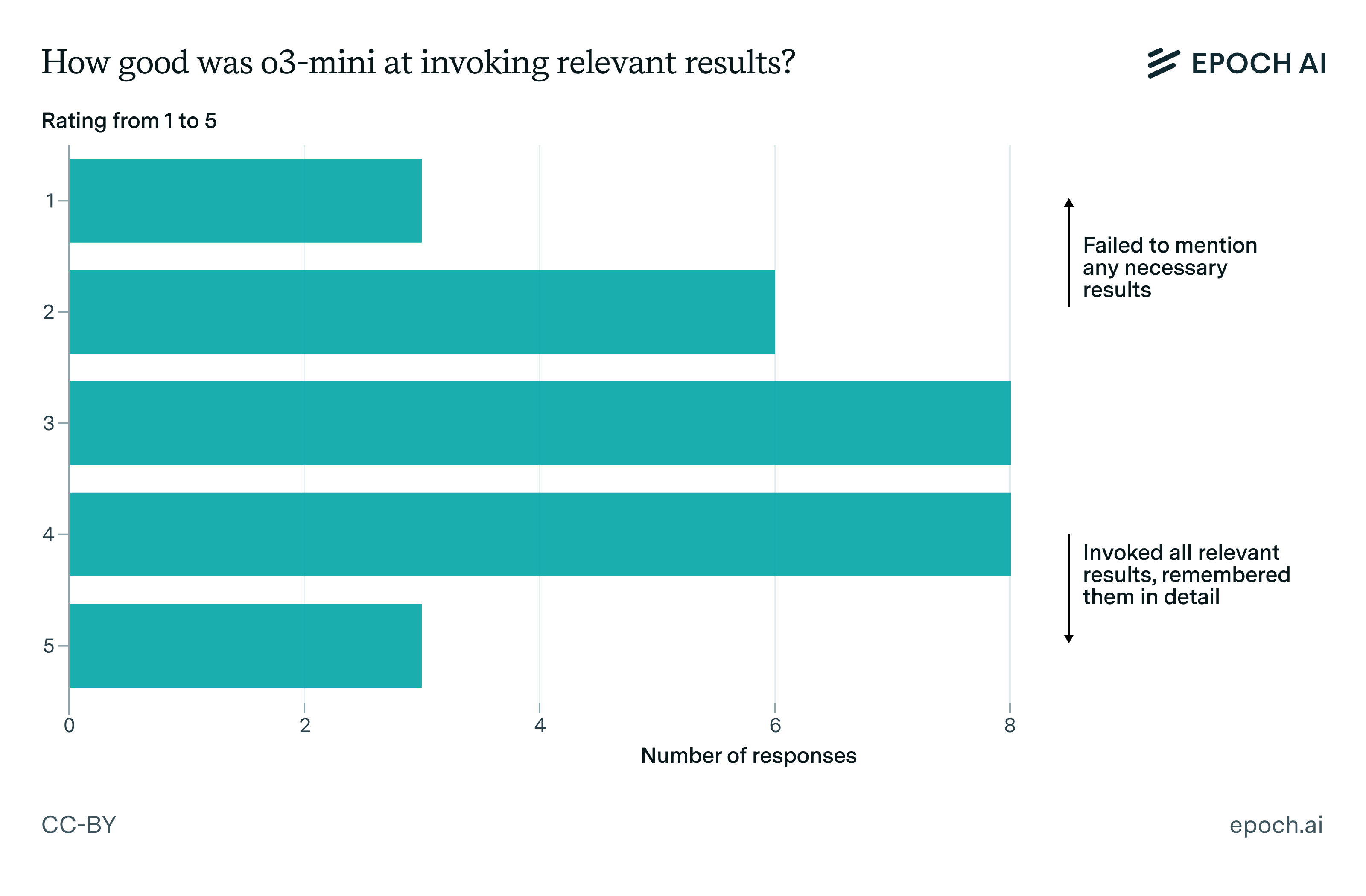
Figure 1: The reviewing mathematicians generally found that o3-mini-high was decent at invoking relevant results from the mathematical literature, achieving a rating of 3/5 or higher on around two thirds of problems.

A “vibes-based inductive reasoner”

Most of the mathematicians also noted that o3-mini-high tends to adopt a pretty informal style of reasoning. One mathematician described the model as a “vibes-based inductive reasoner”, with a “mathematician-like sense of curiosity” that identifies cheap experiments that help get traction on a problem. Another mathematician pointed out that “the model seems to be thinking in a slightly informal, not precise way. The initial formulation of the thought is often rough, the language is not precise, there are some corner cases which would not qualify in a written mathematical paper.”

Why doesn’t the model formalize its reasoning more? It’s not entirely clear to us, but at a minimum we suspect the explanation has to be more complicated than “the model is lazy”. For example, one mathematician noted that “the model is not afraid to compute and write code when needed.” This is a tedious step that helps the model remain more grounded and less abstract, despite being overall quite “vibes-based”. It’s also possible that what mathematicians mean by “formal reasoning” is in fact underrepresented in pre-training data, and only imperfectly evoked in post-training.

Where o3-mini-high fails

Lack of precision

The lack of formal precision we alluded to in the previous section is also one of the main areas where o3-mini-high falls short. For example, one mathematician noted that “where [o3-mini-high] falls well short of a human mathematician is that it does not follow up on a discovery by trying to prove it”. In one case they found that the model makes a correct conjecture through its informal reasoning, “but does not even attempt to prove that conjecture. Instead it just applies the conjecture to solve the problem, getting the correct answer.”

We call such a situation “cheesing”, where a model essentially guesses an answer without going through all the intended reasoning, which in this example would have involved proving the relevant conjecture.² Of the reasoning traces yielding a correct answer, cheesing occurs in a substantial minority:

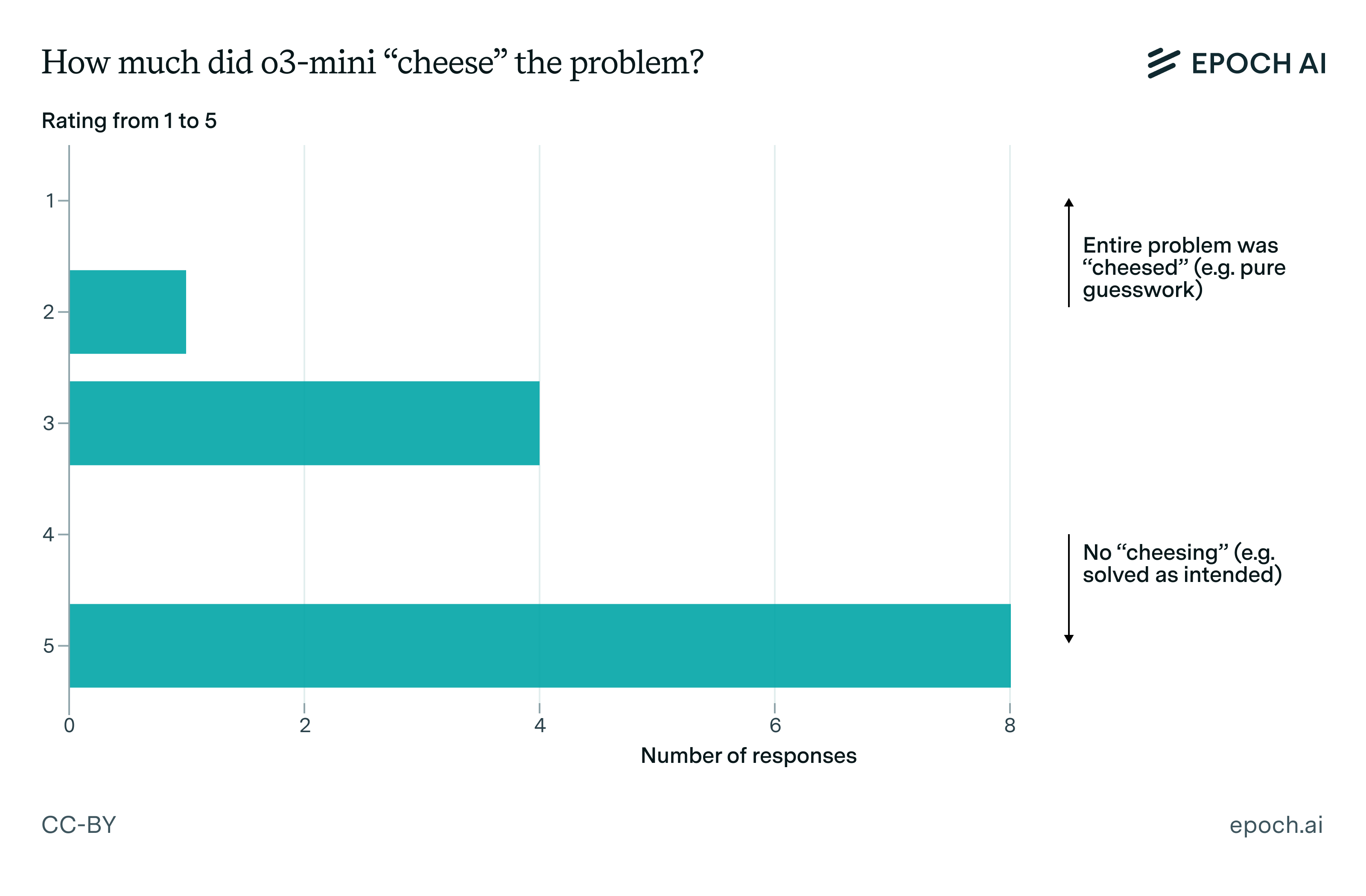
Figure 2: “Cheesing” the problem (not solving the problem as intended) was fairly common, but more often than not o3-mini-high correctly solved the problem without any cheesing at all (i.e. a score of 5). Note that this graph only pertains to reasoning traces where o3-mini-high correctly answered the problem in question.

Sometimes, o3-mini-high was broadly on the right track and didn’t arrive at a correct answer simply because it failed to make a final crucial connection. One partition theory problem for instance was one key step from being answered correctly, with the author stating “If only it summed the outputs from n=0 to [redacted]. The answer would have been correct. I am so impressed by this.”

It was more often the case that o3-mini-high didn’t get this close to cracking the problem, as illustrated in the following graph:

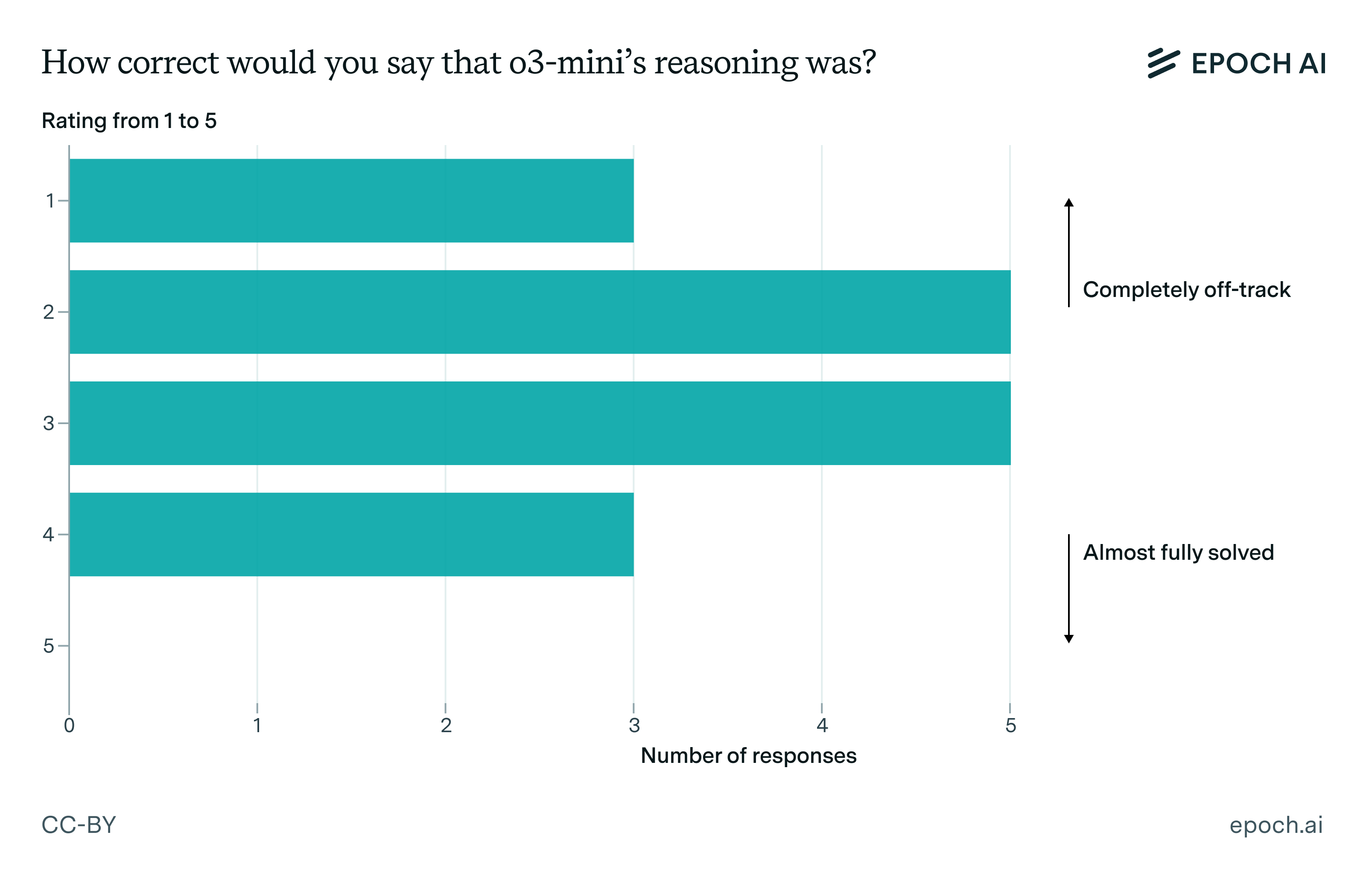
Figure 3: Only around 18% of the cases where o3-mini-high arrived at an incorrect solution were very close to being correct – overall there was more of a spread in how correct the reasoning was.

Lack of creativity and depth of understanding

Arguably the biggest limitation of o3-mini-high that the mathematicians identified is a lack of creativity and depth of understanding, especially compared to a similarly knowledgeable human. One of the mathematicians summarized this picture as follows:

“The model often resembles a keen graduate student who has read extensively and can name-drop many results and authors. While this can seem impressive initially, it quickly becomes apparent to experts that the student hasn’t deeply internalized the material and is mostly regurgitating what they’ve read. The model exhibits a similar behavior—good at recognizing relevant material, but unable to extend or apply it in a novel way.”

Another mathematician said the following:

“The model had a small number of its favourite ideas which it tried to apply. […] Once this handful of ideas was exhausted, there was no real progress. I find it really sad, and from a professional combinatorialist I would expect some more creative attempts to tackle the problem or to frame it differently (even if these attempts would fail).”

One mathematician even went so far as to say that “arguably, AI will find it more difficult to solve a math Olympiad problem for 8th graders, where a new idea is needed, than computing the number of points on some hyperelliptic curve over a large finite field.” Whether or not this is literally true, this is describing the same broad phenomenon as what most of the mathematicians observed.³

Hallucinations

The model also showed many other failure modes. One notable issue was that around 75% of the reasoning traces contain hallucinations, often misremembering mathematical terms and formulas. For example, one mathematician noted that

“While it often recalls the names of relevant formulas, it fails to reproduce them accurately, frequently inserting placeholders like “(…)” where it cannot recall details.”

o3-mini-high also seemed to have issues using libraries and tools, such as internet search. For example, the model was described as trying “to fetch information from many nonexistent URLs that it hallucinates”. This is relevant for instance when it comes to accurately stating very obscure mathematical results in precise fashion. Indeed, one respondent thought that “an agent-like system able to do things like browse Google or the arXiv for potentially relevant results would go a long way towards improving their performance in actual problems.”⁴

Does o3-mini-high reason like a human mathematician?

Given all that we’ve seen above, how similar is o3-mini-high’s reasoning to that of a human mathematician? Overall there seemed to be some variance in the answers to this question, depending on the mathematician and the specific reasoning trace.

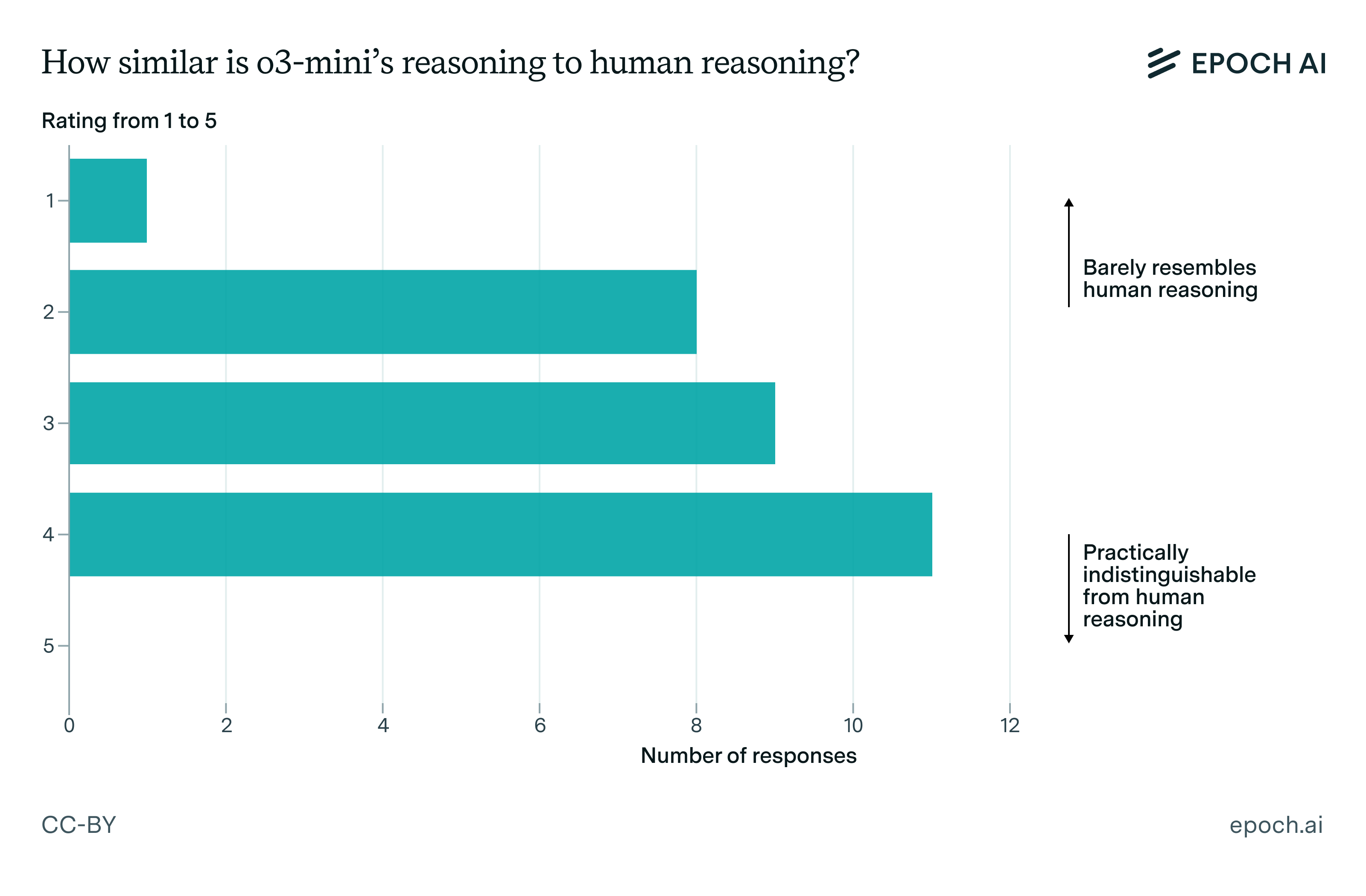
Figure 4: Mathematician ratings of how human-like o3-mini-high reasoning is. A score of 1 corresponds to reasoning that is not human-like at all, and a score of 5 corresponds to reasoning that is indistinguishable from a human mathematician.

We think much of this variance in opinion is due to o3-mini-high having a pretty eclectic mix of capabilities, at least for a human. On the one hand, it seems very capable of reasoning about problems like a human, demonstrating signs of curiosity and exploring different lines of attack on a problem.

On the other hand, it seems perhaps overly knowledgeable, lacks creativity and formality, and also has some strange quirks. For one, o3-mini-high has a tendency to have very wordy reasoning traces, which one mathematician described as “kind of like a very verbose student during an oral exam - not a bad strategy”.

But not all of this wordiness is clearly useful – one respondent pointed out that “the model is oddly neurotic about submitting its final answer”. One example of this is where o3-mini-high “spirals into a repeating loop of rephrasing the sentence that it’s done and now definitely the final answer is the above, occasionally punctured by episodes of self-doubt where it re-calculates step-by-step some arithmetic going into the final formula.” At least in cases like these, the model’s reasoning trace can seem clearly unlike that of a sober human mathematician.⁵

Discussion

Based on the above, we can pithily summarize o3-mini-high as an “erudite vibes-based reasoner that lacks the creativity and formality of professional mathematicians, and tends to be strangely verbose or repetitive”, and this seems to broadly match the opinions of mathematicians we’ve seen online.⁶

We think this analysis naturally leads to two important questions.

First, why do reasoning models like o3-mini-high have these properties in the first place? Part of this is trivial – clearly the models are erudite because they’ve been trained on so much data, including much of the public corpus of math literature. But it’s more mysterious to us why these models aren’t able to capitalize on this knowledge more substantially, making more connections between different subfields of math, creatively coming up with new ideas, and so on.

Second, how much will reasoning models improve on their current weaknesses, such as creativity and formal reasoning? And how much will this change future reasoning traces? One could for instance draw a contrast between the reasoning approaches of o3-mini-high and systems like AlphaProof, where the latter was trained largely (if not entirely) on synthetic data and so has seen a very different data distribution. Given how amenable math is to synthetic data, we think it’s reasonable to expect future reasoning models to less closely resemble human mathematicians.

Of course, what we did here only scratches the surface of the kinds of analysis we could do to understand how these reasoning models work, and we hope to do more of this in the future.

We would like to thank OpenAI for sending us the reasoning traces that made this analysis possible.

Notes

1. The results in this post are based on an evaluation performed by OpenAI, running o3-mini-high on a subset of FrontierMath with their own scaffold. These raw, unfiltered reasoning traces (that we’re usually unable to access) were then sent to us. Note that we don’t have access to all of the reasoning traces, and also don’t have access to the code or tooling used to run these evaluations, so the overall model performance is likely to be different compared to those that we report in our own evaluations on our Benchmarking hub. ↩

2. This is possible on FrontierMath because the problems have answers that can either be expressed numerically or as Sympy objects. Although the problems were designed to be guessproof, this results in a potential weakness where AI systems can “cheese” the problem. ↩

3. This also corroborates with observations that people have publicly made. ↩

4. This is also a direction that models are heading towards – e.g. o3, o4-mini, and Gemini 2.5 Pro support tool use. ↩

5. Though to be fair, humans usually can’t have their full chain-of-thought read out loud, and are possibly quite neurotic internally (or even externally!). But we doubt that it’d look quite the same as the fully repetitive loop that some of the mathematicians came across, so the point still stands. ↩

6. That being said, there are potential issues with a lack of faithfulness of the model’s reasoning, which we didn’t prioritize looking into for the purposes of this survey. ↩