Introduction

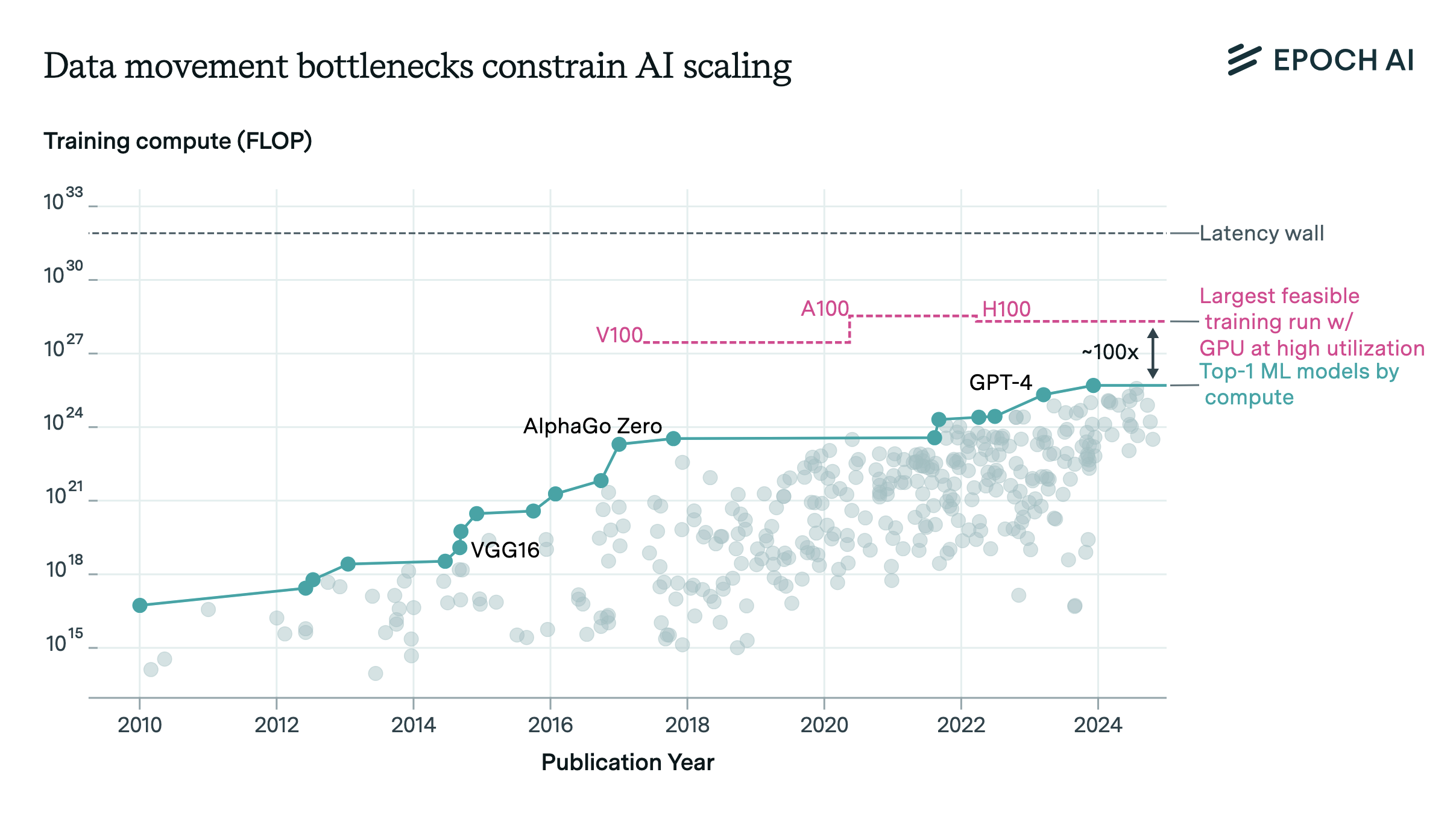
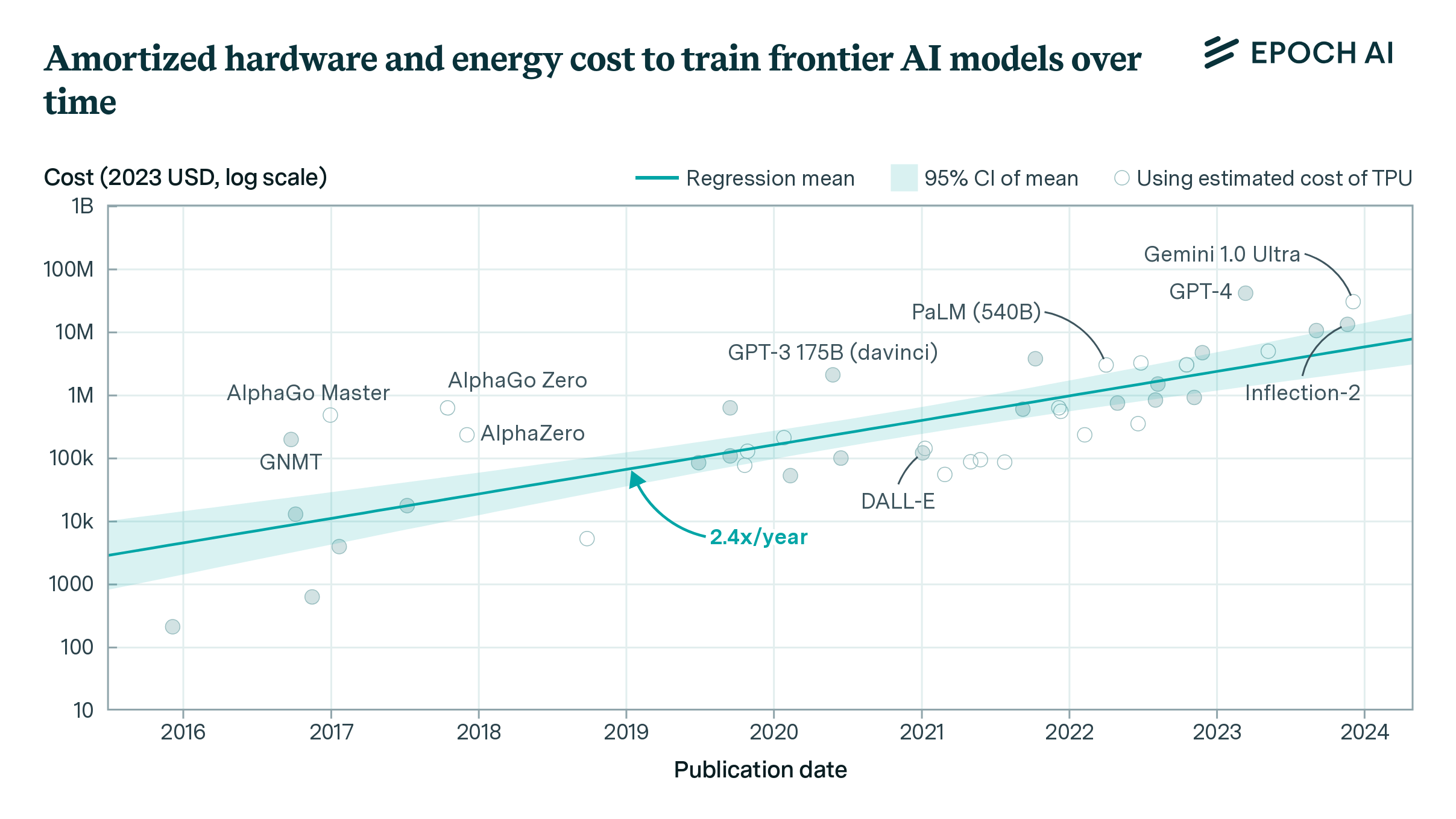
Computational power has become the primary driving force in the race for improved model capabilities. Leading tech companies (Google, Microsoft, Meta, and Amazon) already possess AI computing infrastructure equivalent to more than two million NVIDIA H100 GPUs, and frontier AI model training costs are projected to exceed $1 billion per model by 2027. This scale of computation brings with it an increasingly important challenge in distributed computing: hardware failures.

To understand why, consider that if a single H100 GPU fails on average once every 50,000 hours (about 6 years), a cluster of 100,000 GPUs will face a failure every 30 minutes, and a million-GPU cluster will see failures every 3 minutes.

To combat these failures, engineers resort to one crucial technique: checkpointing. Checkpointing saves training progress to a resilient storage, and in the event of a failure, training can restart by loading saved progress into a working set of GPUs. This opens up an opportunity for optimization, as excessively frequent checkpointing wastes valuable computation time, while insufficient checkpointing risks losing significant progress in the event of a failure.

In this work, we analyze the impact of hardware failures and checkpointing strategies on AI model training time as training clusters scale to millions of GPUs. We develop mathematical models to determine optimal checkpointing intervals and demonstrate that traditional, storage-based checkpointing techniques can limit the scale of training runs if storage is not scaled appropriately.

However, alternative techniques could overcome these limits. We demonstrate that by leveraging distributed memory across training peers for failure recovery—rather than relying on storage-based checkpointing—hardware failures do not practically constrain the size of training runs. This conclusion holds even when considering future model sizes through Chinchilla-optimal scaling laws. We further show that while catastrophic failures, maintenance and potential shifts toward more efficient communication patterns can affect checkpointing strategies, they will not limit AI scaling.

Background and Current Practices

The relationship between system scale and failure frequency creates a critical threshold where checkpointing overhead surpasses productive training time. Consider the scaling pattern: a single H100 SXM GPU fails approximately once per 50,000 hours,¹ but this rate scales linearly with hardware count. Consequently, a system with 16,384 GPUs experiences a failure every 3 hours on average, while a larger system with 1 million GPUs faces a failure every 3 minutes.²

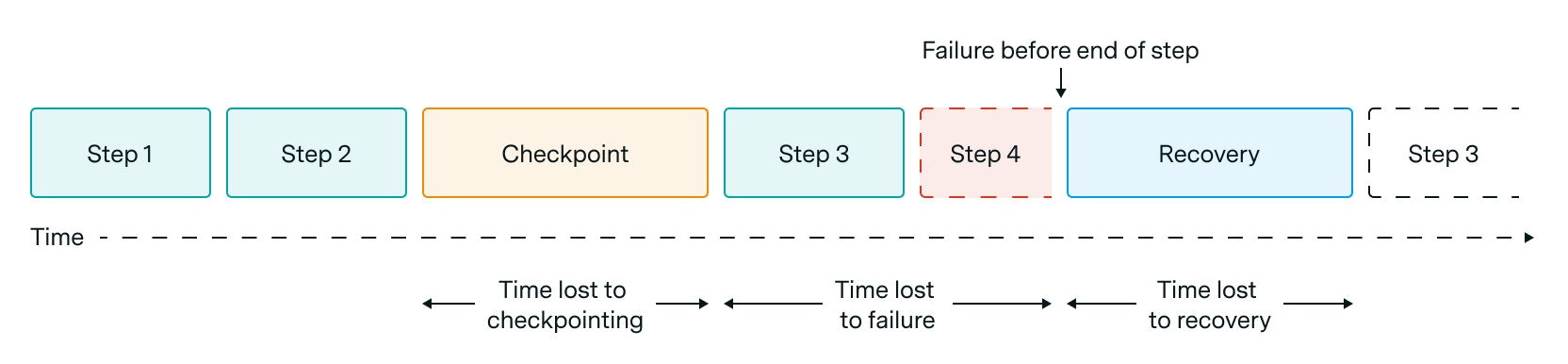
Figure 1: Visualization of how checkpointing, failures, and recovery time lead to lost time.

Training disruptions due to GPU failures involve three distinct time costs (Figure 1): the overhead of saving checkpoints to resilient storage, the lost progress since the last checkpoint, and the system recovery process (including hardware replacement, job reintegration, and checkpoint loading).

A fundamental tradeoff exists in checkpoint frequency: while more frequent checkpoints minimize progress loss from failures, they increase computational overhead. Using a Poisson process to model failure arrivals, we can estimate the expected time lost to failures during computation periods.

We model the total time lost to failures as \(L(t)\) which is a function of \(t\), the time between checkpointing. It consists of two terms: First, the fraction of time spent checkpointing \(\frac{c}{t}\), which is a ratio of \(c\), the time lost to checkpointing, and (e.g., saving the checkpoint takes 5 seconds every 10 minutes). Second, the amount of time lost due to recomputation when a failure occurs, which is a function of the GPU count (\(g\)), the per GPU failure rate (\(\lambda\)), (e.g., \(\lambda = 1/50000\text{h}\)) and the average time lost \(t/2\) as failures are equally likely to happen at any point of the duration \(t\) between two checkpoints.

This results in the total percentage of time lost:

\[L(t) = \frac{c}{t} + \frac{g \lambda t}{2}\]

To find the minimum time lost as a function of \(t\), we can differentiate and solve the equation:

\[\frac{dL}{dt} = -\frac{c}{t^2} + \frac{g \lambda}{2} = 0 \implies t = \sqrt{\frac{2c}{g\lambda}}\]

This formula provides us with the optimal checkpointing frequency \(1/t\), and by plugging the result into \(L\), we can calculate the percentage of time lost.³,⁴

Applying this model to Meta’s Llama 3.1 405B training run⁵, we estimate that approximately 2.1% of total training time was spent on checkpointing and failure recovery, with optimal checkpointing occurring every 4 minutes and taking 2.5 seconds.⁶ This roughly translates to a 1% MFU loss over the entire training duration.⁷

To understand when checkpointing at these speeds will limit further scale, we can examine scenarios where system scale pushes checkpointing duration close to the failure interval. At this point, a problematic cycle emerges: the system increasingly dedicates time to checkpointing and recovery instead of actual training. Eventually, the system might spend more resources managing failures than advancing the training process, potentially making large-scale training infeasible. With Llama 405B as a fixed-size model example and its 2.5s checkpointing speed, when naively increasing the GPU count while keeping both the model architecture and rest of the training setup identical, this becomes an issue at around 70 million GPUs, where the system spends more resources managing failures than advancing training.⁸

In Meta’s case, the checkpointing performance is primarily constrained by a storage bandwidth of 2TB/s when writing optimizer states. Recovery time requires even higher bandwidth due to data-parallel training, where multiple GPUs must read partially duplicate optimizer states. While exact recovery bandwidth requirements vary with different sharding strategies (ZeRO-1,2,3), a naive estimate based on the number of data-parallel ranks suggests a recovery time of approximately 5 minutes.⁹

Although present checkpointing overhead doesn’t significantly limit AI scaling, the storage interconnect could become a bottleneck as model and cluster sizes grow larger. This raises an important question: are there checkpointing strategies that entirely bypass the need for dedicated, resilient storage?

Alternative Checkpointing Strategies Using GPU Memory

Instead of relying on traditional storage systems for checkpointing, we consider two approaches that leverage GPU memory directly to handle failures. The first approach eliminates checkpointing entirely, relying instead on data-parallel replicas for recovery. The second approach distributes checkpointing data across the cluster, storing each GPU’s state in the memory of other GPUs in the cluster. Recovery then occurs by using an already provisioned node kept in a buffer that reads directly from the replicated peer GPU memory rather than from storage—Google DeepMind described using a similar strategy while training Gemini.

Both techniques rely on redundant GPU memory for fault tolerance. While one method uses sharding to maintain GPU replicas, the other employs explicit checkpointing. We’ll focus on the checkpointing approach since it operates independently of the training configuration, unlike sharding, which may adjust the parallelization setup to varying context lengths and can make it harder to ensure complete replication of each GPU state.¹⁰

Meta’s Llama 405B training demonstrates that the approach of checkpointing to GPU memory is viable at the current frontier of training. Concretely, the Llama 3.1 team reported only 4 GB of checkpointing memory used per GPU. This leaves approximately 76 GB free per GPU for activations, gradients, and potential storage of other GPUs’ checkpoint data. Since compute requirements scale quadratically with model size while memory scales linearly, the resulting quadratic growth in GPU count (and thus total memory) will always exceed checkpoint storage requirements.

The effectiveness of these failure handling approaches depends on the replication factor \(M\), since GPUs storing the copies may themselves fail. Given failures follow a Poisson process with node failure rate \(\lambda_{\text{node}}\), the probability of failure during a training step \(t_{\text{step}}\) is:

\[1 - e^{-\lambda_{\text{node}} t_{\text{step}}} \approx \lambda_{\text{node}} t_{\text{step}}\]

See ¹¹ for the approximation

To understand the required replication factor, we can model the expected number of failures \(F\) over the entire the training run \(t_{\text{train}}\). Even one of these failures would stop the training, as a complete group of \(M\) GPUs would fail, making recovery impossible:

\[F = \frac{t_{\text{train}}}{t_{\text{step}}} \cdot \frac{N_{\text{GPU}}}{M} \cdot (\lambda_{\text{node}} t_{step})^M\]

The key intuition here is when we increase the replication factor \(M\), we’re requiring multiple independent failures to happen simultaneously to lose our data. This becomes exponentially less likely with each additional replica. For example, with 1000 GPUs grouped by 8 in a DGX node, running for 60 days (\(t_{\text{step}} = 10\text{s}\), \(\lambda_{\text{node}} = 1/8000\text{h}\)), having just two backup copies (\(M=2\)) would result in a failure every 533 training runs. But with three copies (\(M=3\)), the expected failures plummet to roughly one failure every 2.3 billion training runs. Since each additional replica multiplies this safety factor, using \(M=4\) copies makes catastrophic failure extremely unlikely.

Given that we can exclude independent replica failures, how fast can we checkpoint and recover with these approaches? As checkpointing incurs a broadcast to \(M=4\) peers and recovery only needs a single peer to be available, we focus on checkpointing as the limiting operation. We can solve for the amount of GPUs needed such that the expected time to failure is equal to the time spent checkpointing when using the H100 DGX network interconnect of 400Gb/s:

\[\frac{50000 {\text{h}}}{N_{\text{GPU}}} = \frac{M \cdot 4\text{GB}}{400 \text{Gb/s}}= \frac{16\text{GB}}{50 \text{GB/s}} = 0.32 \text{s} \implies 562\text{M GPUs}\]

This is an 8x improvement in checkpointing speed compared to the previous 2.5s when writing to resilient storage, and increases the feasibility of the theoretical training run from 70M to approximately 560M GPUs.

Chinchilla-based Model Sizes

While the Llama 405B training run provides an estimate for current model sizes, you would not train a model of this size on a cluster with millions of GPUs—you would instead leverage the larger cluster to train a larger model in the first place. Given this, a more general model for the amount of GPUs is needed that takes different model scales, networking topologies and optimized data movement into account.

First, replicating multiple copies of each GPU shard across the cluster is not necessary, as we can only replicate one complete optimizer state defined as \(S_\text{opt} = N_\text{param} \cdot N_\text{optimizer} \cdot N_\text{bytes}\), including the precision and the optimizer state factor.¹² This optimizer state must be replicated to \(M\) peer nodes, resulting in a total network load of \(M \cdot S_\text{opt}\) across the entire cluster.

This replication speed is limited by total cluster read bandwidth; with current systems designed for all-to-all GPU communication, that assumes a linear relationship between GPU count \(N_{\text{GPU}}\) and total bandwidth \(B_{\text{total}}\). However, as clusters scale to millions of GPUs, this relationship may shift due to new switch-level aggregation hardware or training approaches that prioritize local over all-to-all communication. To account for these potential future scenarios, we analyze both linear (\(\alpha = 1\)) and square-root (\(\alpha = 0.5\)) scaling relationships in \(N_{\text{GPU}}^{\alpha} \propto B_{\text{total}}\). Despite specialized hardware like NVIDIA’s NVLink for Blackwell achieving 900 GB/s in small clusters (up to 600 GPUs), we use a conservative 50GB/s GPU-to-GPU interconnect speed and find that both scaling assumptions lead to the same conclusions about system scalability.

\[\frac{50000 {\text{h}}}{N_{\text{GPU}}} = \frac{M \cdot S_\text{opt}}{50 \text{GB/s} \cdot N_{\text{GPU}}^{\alpha}}\]

Second, we can define the model size dependent on the amount of GPUs, as, when following Chinchilla scaling, compute \(C\) is proportional to the amount of parameters squared \(C = 120 \cdot {N_{\text{param}}}^2\).¹³,¹⁴ Using this relationship, we can determine the optimal number of parameters based on three variables: the peak GPU FLOP/s (\(C_{\text{peak}}\)) times the GPU utilization ratio (\(\text{MFU}\)) and \(N_{\text{GPU}}\):

\[N_{\text{param}} = \sqrt{\frac{N_{\text{GPU}} \cdot C_{\text{peak}} \cdot \text{MFU}}{120}}\]

Plugging in the H100 SXM’s 989 TFLOP/s and an MFU of 50% gives us the simple equation:

\[N_{\text{param}} = 2e6 \cdot \sqrt{N_{\text{GPU}}}\]

Combining this GPU-dependent model size equation and setting \(M=4\), \(N_{\text{optimizer}}=3\), \(N_{\text{bytes}}=4\), we can solve for \(N_{\text{GPU}}\):

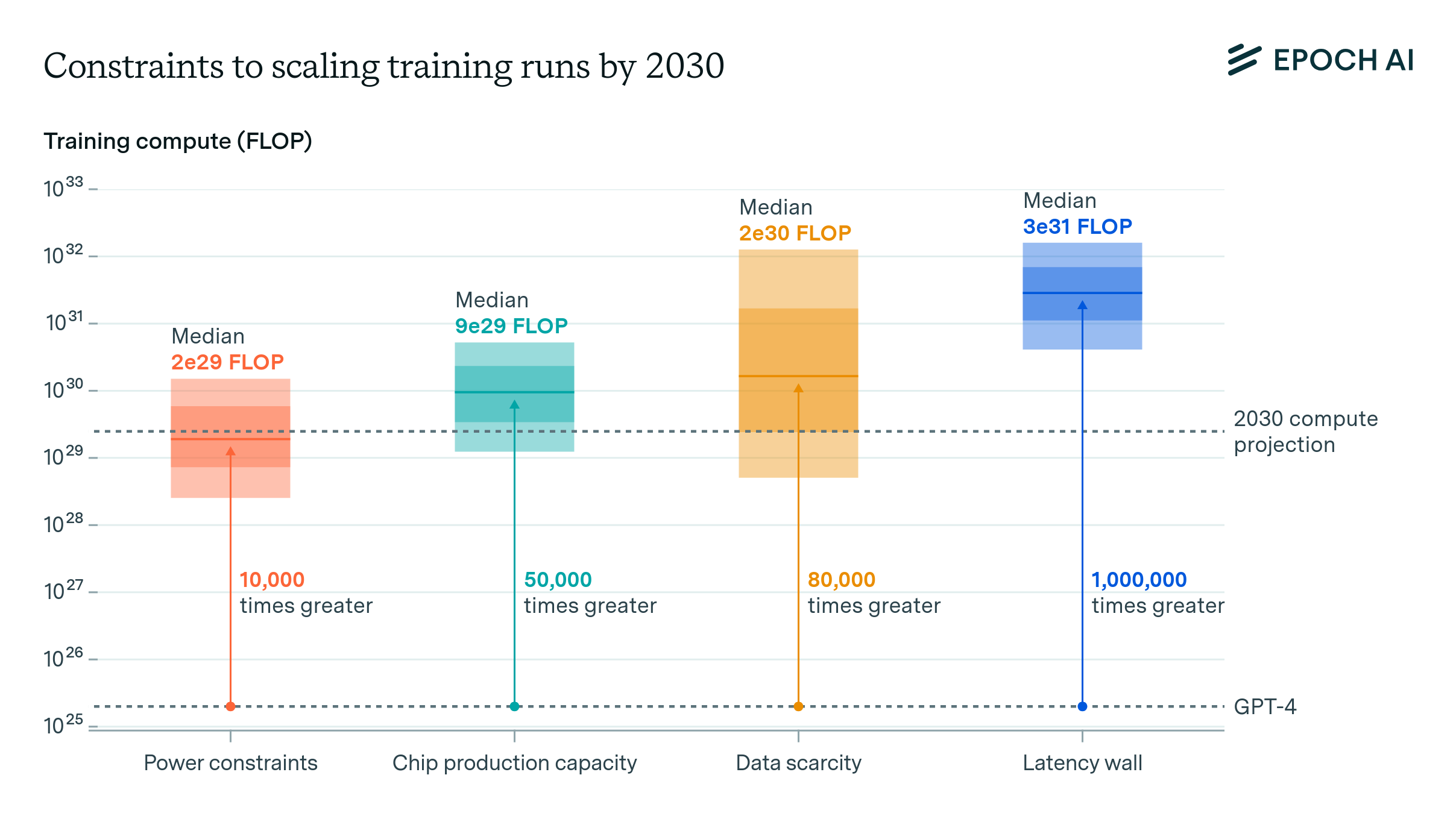
\[\frac{50000\text{h}}{N_{\text{GPU}}} = \frac{48 \cdot 2e6 \cdot \sqrt{N_{\text{GPU}}}\text{ byte}}{50 \text{GB/s} \cdot N_{\text{GPU}}^{\alpha}}\] \[\alpha = 1 \implies N_{\text{GPU}} \approx 9e21 = 9 \text{ sextillion GPUs}\] \[\alpha = 0.5 \implies N_{\text{GPU}} \approx 94e9 = 94 \text{ billion GPUs}\]

With current hardware specifications, the maximum number of GPUs sustainable before failure rates match checkpointing time ranges from billions to sextillions. This limit is governed by the relative scaling of compute versus network interconnect, where bandwidth scaling (characterized by \(\alpha\)) plays a crucial role. While our analysis assumes replication through the top-level switch—necessary only for protecting against localized failures like rack-wide power losses—practical implementations would favor nearby-node replication. This local replication approach supports linear bandwidth scaling, leading us to conclude that hardware failures pose no meaningful constraint for limiting future large-scale training.

Idle Spares, Maintenance and Catastrophic Failures

While hardware failures will not theoretically limit scaling under current training practices, the engineering challenges remain significant. In practice, provisioning new nodes from scratch can take hours, yet in million-GPU clusters, failures occur every few minutes, requiring instantly available replacements from a buffer of idle nodes that wait to be used. However, this buffer can be relatively small through continuous replenishment: with 20 node failures per hour in a 1M GPU cluster (125K nodes) and a pessimistic one-day replacement time, a buffer of 480 nodes (0.3% of capacity) suffices. Even if replenishment takes several days due to manual intervention requirements, the performance impact remains below 1%, negligibly affecting training time.

Optimizing further, these idle spares can run preemptible low-priority workloads to maintain cluster utilization. However, the effectiveness of this approach depends on job orchestration systems (e.g., SLURM, Kubernetes, MAST) and their preemption and deployment performance.

Cluster maintenance presents another challenge, requiring regular updates to drivers, kernels, and libraries. Meta performs these updates in the form of a “maintenance train” by updating a few nodes at a time and incorporating them back into the cluster fleet. These scheduled updates happened roughly once per day over the total training duration of Llama 405B.¹⁵ However, the synchronous nature of AI training requires homogeneous nodes, ultimately necessitating checkpointing to resilient storage during updates. This operational constraint is not expected to limit future scaling, as the system already uses robust checkpointing mechanisms for failure recovery, which can be reused for maintenance windows regardless of the checkpointing duration to resilient storage.

Beyond hardware failures, which scale with cluster size, other failure modes warrant consideration. While some failures do not have this scaling property (e.g., bugs introduced by software), others can become more likely due to the sheer size of the cluster. Earthquakes, hurricanes, electrical power outages, cosmic rays, and even fires are not accounted for. Memory-based replication makes individual hardware failures negligible, making these systemic risks the primary concern. Addressing them requires remote storage-based checkpointing, which affects training speed only during checkpointing rather than fundamentally limiting scale.

Conclusion

In this article, we estimated the effect of hardware failures on the largest possible training run by analyzing current and future checkpointing strategies and their interplay with model and cluster scaling. Our main result: Assuming Chinchilla-based scaling is roughly followed and failure rates stay similar to once per 50,000 GPU-hours, checkpointing will not limit the scale of AI training runs, at least not in the near or medium-term future.

We find that failures become critical to training progress at 70 million GPUs with current checkpointing strategies that use resilient storage solutions. This is pushed further to 560 million GPUs when leveraging abundant GPU memory capacity to store checkpoints with current hardware and model sizes. When considering future model scales or changes to current training paradigms, we find no practical upper bound on cluster size that would meaningfully impact training feasibility.

This conclusion has three implications: First, hardware failures will not limit AI training scalability, even as communication patterns evolve beyond current all-to-all approaches. Second, storage infrastructure can be optimized primarily for training data ingestion rather than checkpointing, as high-bandwidth storage systems are no longer critical for failure recovery. Finally, while our theoretical analysis shows ample headroom for scaling, significant engineering work remains to fully implement these GPU memory-based checkpointing techniques—currently demonstrated only by Google.

Acknowledgements

We want to thank Robi Rahman, Jaime Sevilla and Tamay Besiroglu for their research advice. Special thanks to Robert Sandler for designing the figures and splash visual and Andrew Souza for web development.

Appendix A - General Checkpointing Model

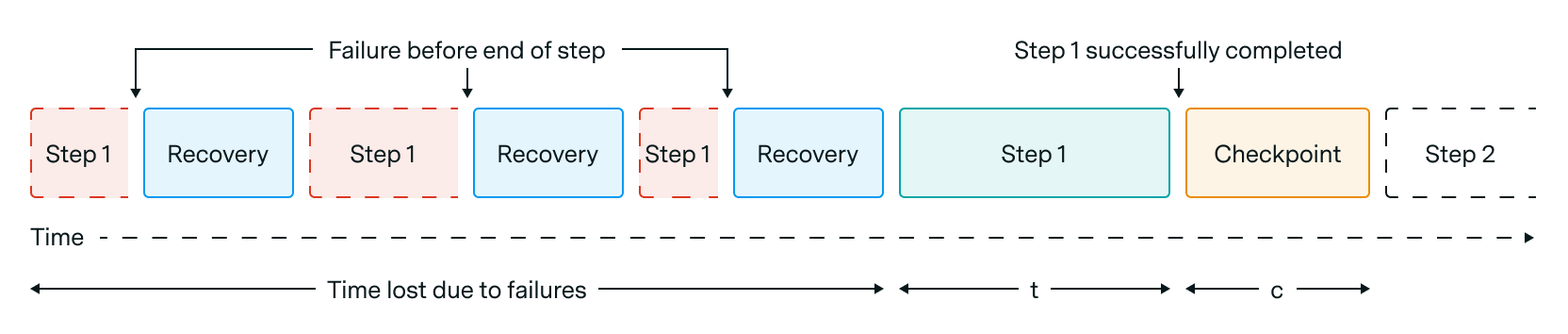
Figure 2: If the expected time to failure (\(g \lambda\)) is shorter than the average time between checkpoints (\(t\)), the average time lost is a sum of all recomputations due to failures.

The approximate model in the main article breaks down when the expected time to failure \(g \lambda\) is lower than \(t\), the time between checkpoints. If failures happen multiple times during a single interval of useful work, the average time lost is not \(t/2\) but rather a sum of the redundant computation until a single atomic step successfully completes (Figure 2). A general way to model this behavior is by explicitly capturing the time spent on failures that happen multiple times before a checkpoint is reached, which we detail here.

Suppose the time until the next failure follows an exponential distribution with mean \(1/\lambda\), and our checkpointing time interval is given by \(t\), and we lose time \(c\) for every checkpoint.

Then, to make it from one checkpoint to the next, we will sample variables \(X_k\) from the exponential distribution until we get the first sample such that \(X_k \geq t\), and our time taken will be

\[X_1 + X_2 + ... + X_{k-1} + t + c\]

where \(X_k\) is the first random variable that is sampled to be greater than or equal to \(t\). Since \(k\) is also a random variable, we can express this sum as follows:

\[T = \sum_{i=1}^{\infty} 1_{X_1,X_2,...,X_i<t} \cdot X_i + t + c\]

Taking expected values gives

\[E[T] = \sum_{i=1}^{\infty} E[1_{X_1,X_2,...,X_{i-1}<t}] \cdot E[1_{X_i<t} \cdot X_i] + t + c\]

by the independence of all of the \(X_i\). In closed form, this expected value can be computed as

\[E[T] = \sum_{i=1}^{\infty} (1 - e^{-\lambda t})^{i-1} \cdot \left(\frac{1}{\lambda} - e^{-\lambda t}\left(\frac{1}{\lambda} + t\right)\right) + t + c = e^{\lambda t} \cdot \left(\frac{1}{\lambda} - e^{-\lambda t}\left(\frac{1}{\lambda} + t\right)\right) + t + c\] \[= \frac{e^{\lambda t} - 1}{\lambda} + c\]

This is the amount of time we take per checkpoint when we require \(t\) seconds of “actual progress” to be made between any two successive checkpoints. If our training run is expected to take some fixed amount of useful cluster time, then the number of checkpoints we’ll need to do throughout will be inversely proportional to t, so the total time taken for our training run will be proportional to

\[\frac{e^{\lambda t} - 1}{\lambda t} + \frac{c}{t}\]

Our goal is therefore to pick \(t\) such that it minimizes this expression. Differentiating and setting the derivative equal to zero gives the solution

\[t = \frac{1 + W\left(\frac{c\lambda-1}{e}\right)}{\lambda}\]

where W is the Lambert W function, here interpreted as taking its principal branch values. When the time between failures is much greater than the time we need for each checkpoint to be complete, so that \(c \lambda \ll 1\), we can use the expansion

\[W_0(z) = -1 + \delta + O(\delta^2), \delta = \sqrt{2(ez + 1)}\]

of the principal branch of the Lambert W function around \(-1/e\) (Corless et al. 1996) to get

\[t = \frac{1 + W\left(\frac{c\lambda-1}{e}\right)}{\lambda} \approx \sqrt{\frac{2c}{\lambda}}\]

The parameter \(\lambda\) corresponds to the hardware failure rate of our cluster and can be expressed as \(\lambda = fg\) where \(f\) is the per GPU failure rate and \(g\) is the number of GPUs in our cluster. This gives a reasonable approximation

\[t \approx \sqrt{\frac{2c}{fg}}\]

in the regime \(c \lambda \ll 1\). In the opposite regime of \(c \lambda \gg 1\), we can instead use the asymptotic expansion

\[W_0(z) = \log z - \log \log z + o(1)\]

of the principal branch of the Lambert W function to obtain

\[t \approx \frac{\log(c\lambda) - \log \log(c\lambda) + O(1)}{\lambda}\]

The function modeling the time lost and its derivative can be implemented in Python as follows:

import numpy as np
import math
from scipy import special

def optimal_checkpoint_interval_approx(c, g, f):
    return math.pow(2*c / (g * f), 1/2)

def fraction_time_lost_approx(t, c, g, f):
    return (c / t) + (g * f * t) / 2

def optimal_checkpoint_interval(c, g, f):
    lambda_ = g*f
    return (1 + special.lambertw((c * lambda_ - 1) / np.e).real) / lambda_

def time_lost_percentage(c, t, g, f):
    lambda_t = g * f * t
    return ((np.exp(lambda_t) - 1) / lambda_t + c / t) - 1

c = 2.43 / 3600 # in hours
f = 1 / 50000 # in GPU-hours
g = 16384 # GPUs
t = optimal_checkpoint_interval(c=c, f=f, g=g)
time_lost = time_lost_percentage(c=c, t=t, g=g, f=f)

Notes

1. Meta’s training process for the Llama 3.1 405B model spanned 54 days using 16,384 GPUs, encountering 419 failures throughout the training period. 16384 GPUs x 54 days ≈ 880,000 GPU days, 880,000 GPU days / 419 failures ≈ 2100 GPU days/failure ≈ 50,000 GPU hours/failure. ↩

2. Accurately assessing GPU reliability presents two challenges: failures occur infrequently at smaller scales, and manufacturers rarely disclose failure data. Hardware typically undergoes an initial break-in period with elevated failure rates due to manufacturing flaws or installation issues, making it hard to verify that reported failure rates are representative. Meta’s dedicated AI training cluster provides valuable reliability data for H100 GPUs operating in their stable phase, which is why we use it throughout this article. ↩

3. After deriving this model from first principles, we noticed that this model is identical to one leading back to a publication from 1974 by Young, even though they used an exponential distribution as a starting point to model the time lost. To see the equivalency of the formulas, exchange \(c\) for \(T_s\), and \(g \lambda\) for \(T_f\). ↩

4. This model has the assumption of failures being much less frequent than the interval between failures \(t\), which may not be true in very large clusters. We provide a more general model that includes this consideration in Appendix A. ↩

5. Chosen as an example because this was one of the largest training runs to date, and Meta published extensive training details. ↩

6. The 2.1% time lost comes from plugging in these parameters from the Llama 405B paper into the model. Checkpointing time: 405B x 3 numbers per parameter x 4 bytes = 4860GB, 4860GB / 2TB/s = 2.43s, Failure rate: 1/50000 GPU-hours, GPU-count: 16384 ↩

7. 41% MFU x (100% runtime - 2.1% time lost) = 40.14% ↩

8. 50000 GPU-hours / 2.5s = 72M GPUs ↩

9. 128 DP-ranks x 4860GB optimizer state / 2TB/s / 60s = 5.1 minutes ↩

10. For example, full optimizer sharding (ZeRO-1) will be made impossible, as the optimizer state is equally divided over all GPUs, ensuring that no single GPU is entirely replicated. Even data-parallel setups can change during the training, which can make replication harder to facilitate in practice (e.g., during the training of Llama 405B, Table 4). ↩

11. Taylor series approximation for very small x: \(e^{-x} = 1 - x\), \(1 - e^{-\lambda_{\text{node}} t_{\text{step}}} = 1 - (1 - \lambda_{\text{node}} t_{\text{step}}) = \lambda_{\text{node}} t_{\text{step}}\) ↩

12. AdamW uses 3 numbers per parameter: 1) the parameter itself 2) (\(\beta_1\)), the first moment and 3) (\(\beta_2\)), the second moment estimate. ↩

13. Chinchilla: D = 20N, FLOP estimation C=6ND, C=6N(20N)=120N^2 ↩

14. The economic incentive to reduce inference costs may lead to overtraining relative to Chinchilla-optimal levels, since higher tokens-per-parameter ratios (\(\frac{D}{N}\)) allow for smaller, more efficient models while maintaining performance. This improves checkpointing performance and further strengthens the relevance of our analysis. ↩

15. During the training duration, Meta performed 47 planned interruptions over 54 days. ↩