Recent advances in artificial intelligence are beginning to influence the field of mathematics, prompting important questions about how mathematical research might evolve. Systems like Google DeepMind’s AlphaProof have demonstrated capabilities approaching gold medal-level performance at the International Mathematical Olympiad. Professor Timothy Gowers described these abilities as “very impressive, and well beyond what I thought was state of the art.”

Developments like these raise several important questions: How will the nature of mathematics research evolve over the next decade? Can mathematics research be fully automated, and when might this happen? To answer these questions, we interviewed four distinguished mathematicians about the implications of AI progress in mathematics: Fields Medalists Prof Terence Tao, Prof Timothy Gowers, and Prof Richard Borcherds, as well as IMO expert Evan Chen.

In our conversations, the mathematicians highlighted key themes regarding AI’s potential impact on mathematics. They discussed how AI could assist in proof development and verification, facilitate experimental approaches by exploring vast numbers of potential statements, generate novel conjectures by synthesizing information across fields, reduce barriers to entry into specialized areas through accurate explanations of complex concepts, and enhance error detection in mathematical work. They also contemplated the challenges AI faces in achieving deep research competence, such as acquiring domain-specific expertise and learning from the iterative process of mathematical discovery.

AI augmentation of mathematics research

Although current AI models struggle with research-level problems, the mathematicians identified several ways that AI systems could transform mathematical practice in the coming years.

Proof development/verification. Currently, translating informal mathematical arguments into rigorous, machine-verifiable proofs requires significant effort and expertise in formal systems. With the aid of AI systems, several of the mathematicians felt that bridging this gap could be possible fairly soon. Borcherds surmised that “AI is pretty close to being able to formalize an awful lot of human mathematics,” and Tao pointed out that this ability to formalize statements could be useful in proof development within around five years. “If I were to write a math paper, I would explain the proof to a proof assistant… and they would help formalize it.” Such tools could significantly reduce the time and specialized knowledge required for formal verification while maintaining mathematical rigor.

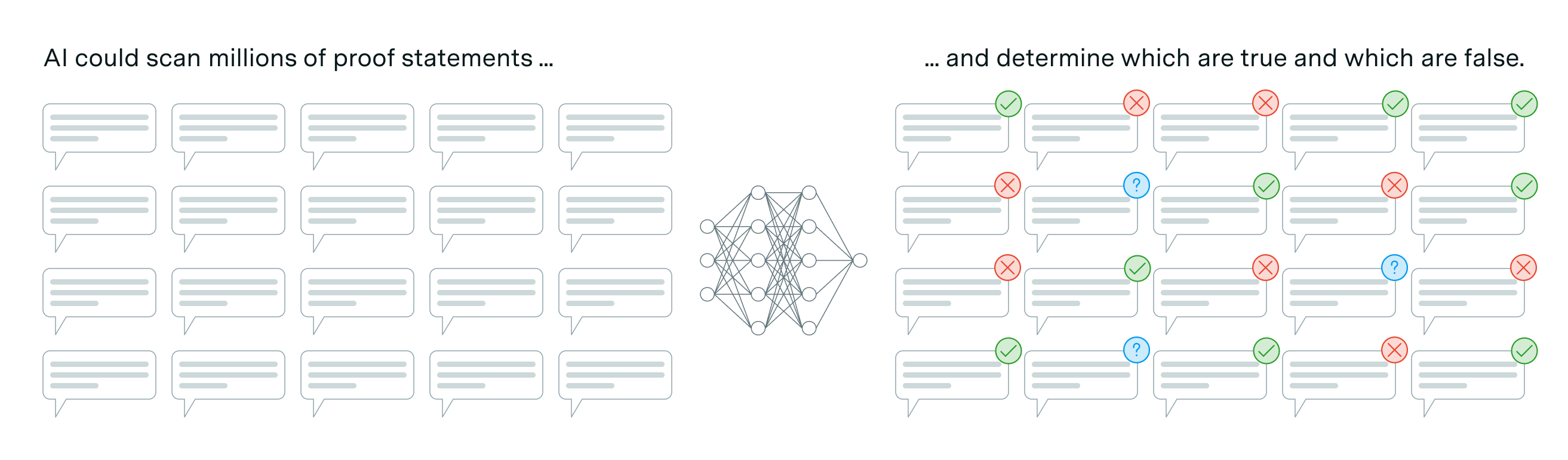
Experimental mathematics. With AI systems that can perform routine proofs at scale, several of the mathematicians envisioned mathematics becoming much more of an experimental science. Tao predicted that AI tools would let researchers “scan a million possible proof statements, see which ones are true and which ones are false and draw empirical conclusions from that… Math is 99% theoretical right now, but only for technical reasons, only for technological reasons.” Gowers captured this transformation with a vivid metaphor: “Your computer becomes the test tube and you sort of stick the problem in the test tube and shake it around and see what comes out.”

Automated conjecture generation. Since AI systems are trained on vast quantities of data across disparate fields, and have the ability to search through the mathematical literature at scale, Chen felt that they could be incredibly effective at automatically generating novel conjectures. “This is a thing I think [large language models] would be really, really good at.” In contrast, Chen argued that humans instead “go to conferences, listen to other people talk, and see if anything by chance manages to line up.”

Entry barriers. Another significant potential impact of AI tools is in making specialized mathematical knowledge more accessible. For instance, Chen pointed out that entering a new field of mathematics currently requires years of background study. With AI assistants accurately explaining core terms and intuitions, however, Chen speculated that the “barrier to entry to fields becomes a lot lower”. Gowers further suggests that AI could perform mathematical techniques “that are at some fundamental level routine, but for most people not routine because they don’t have the relevant expertise in some subdomain of mathematics.” AI systems with this ability could therefore allow researchers to work more fluidly across specialized domains.

Error detection. A significant practical benefit of AI assistance could be in catching mathematical errors. In particular, reviewing mathematical papers can require substantial time, effort, and domain expertise, making it impractical to check most papers in full detail. Chen expects that AI systems could transform this, revealing substantial errors: “[I think if you] took a random sample of the papers on the arXiv, there would just be mistakes everywhere. It would be like code if we didn’t have unit tests.” Combined with the earlier discussion of formal verification capabilities, this suggests AI systems could help ensure mathematical results are more reliable by systematically checking proofs and calculations.

Challenges to AI systems achieving deep research competence in math

A key challenge for AI systems achieving research-level mathematical competence is acquiring deep domain-specific expertise. As Chen observed when discussing advanced mathematics, specialized domains often have “a lack of training material,” with Tao adding that for many research areas “you’re talking a dozen papers with relevant concepts and information”.

Similarly, a critical limitation for AI systems in mathematical research is their lack of exposure to the iterative process of mathematical discovery and learning from failures. While current models can “produce some plausible strategies” for difficult problems, as Tao points out, “[one thing which] current AIs just suck at is, if you try an approach and it doesn’t work, what lessons do you learn from that failure to adjust your strategy.” This deficit stems partly from the bias in mathematical training data—mathematicians “only publish our best proofs of our best theorems”. AI systems therefore miss the crucial learning experiences of graduate education where students “try stupid things to solve a problem” and receive expert feedback on how to adjust their approach. Without these experiences of supervised practice and failure, AI systems might struggle to develop the mathematical intuition that allows experts to identify promising strategies and adapt their approaches based on partial progress.

The mathematicians identified several potential ways of overcoming these data challenges. One approach is to gather data through human-AI collaboration, directly observing human mathematicians correct their mistakes and tackle novel problems. Another is to leverage formal verifiers to generate large quantities of synthetic data, similar to the approach used in Google DeepMind’s AlphaProof. An additional possibility, not mentioned by the interviewees, is to use reinforcement learning to train models to hone their chains of reasoning. This is the approach implemented in OpenAI’s o1 model, and helps models learn to identify and fix mistakes, as well as decompose complex problems into simpler ones. However, whether these techniques will be sufficient to overcome the aforementioned challenges remains to be seen.

Fully automating mathematics research

When might AI systems be capable of automating most mathematical research, discovering and proving novel theorems without human oversight? First of all, all of the mathematicians agreed that such a scenario was possible in principle. For example, Borcherds emphasized that “there will be a short phase when humans and AI are interacting to produce proofs, I would guess. But then eventually you’ll reach a point where the AI is so good that human intervention just makes it worse.” Gowers felt similarly, expecting that “there’d be a certain point where AI can do [everything a human mathematician] does and that would take the human out of the loop.”

This is in stark contrast to the view that AIs will not be able to perform certain mathematical tasks, such as because of a lack of true “understanding” on the part of the AI systems. Borcherds however expressed skepticism about this position: “I’m not going to place too much weight on mathematicians who claim there are things AI will never be able to do because they don’t really understand… The same thing was happening 20 or 30 years ago with chess. […] I talked to a few very strong chess players who said that there are things that computers will never understand about chess; that they’re going to reach a wall fairly soon – and this never happened. The computers just kept on getting better and better, and there wasn’t any fundamental wall of understanding. […] So I wouldn’t be surprised if the same is true for mathematics.”

But when might AI systems surpass human capabilities in mathematics research, as they did in chess? Borcherds expected roughly 10 years until AI surpasses human capabilities, but with substantial uncertainty. “When is AI going to overtake humans at research? Well, not in the next year, and almost certainly in the next 100 years. So I’ll go for about ten years or so.”

Tao was slightly more skeptical. He felt it was very unlikely that AI would be able to perform math research unassisted within three to four years: “I don’t see that happening. I think we would need a lot of experience with the hybrid model [with human-AI collaboration] first.” That said, he agreed that full automation might be theoretically possible within a decade with massive investment, via something akin to a “Manhattan project” for automated math research.

The interviews clearly show that there is a great deal of uncertainty about when and how math research will be automated. This depends on a range of complex factors, such as the feasibility of continued AI scaling and data availability, both of which we’ve touched upon in our research.

To help shed light on these important topics, we’ve developed FrontierMath, a benchmark of extremely challenging math problems designed by over 60 mathematicians. Unlike most existing math benchmarks, FrontierMath captures a broad range of topics in modern mathematics, including research-level topics. While solving the benchmark problems is not quite the same as constructing original proofs, we believe that FrontierMath is a significant step forward in tracking AI progress in mathematics.

In the future, we hope to analyze how model performance on FrontierMath scales with compute and training data, and what this means for future rates of progress. We’ll also be continuing our work on developing challenging benchmarks and tracking key trends in AI progress, both in mathematics and beyond.

Conclusion

Although there remains substantial uncertainty about AI’s future role in mathematics, our interviews with mathematicians help shed light on some of the possibilities. In the next few years, they described the possibility of more experimental approaches to mathematics, formalization of mathematical statements, and reduced barriers to entry. In the longer run, there was broad consensus that automating math research is possible in principle, although this is likely to be preceded by a period of human-AI collaboration and may require overcoming data limitations. In all cases, the mathematicians described a future of math research transformed by the use of AI systems, and time will tell whether their visions turn out to be right.