Summary
Hoffmann et al. (2022) investigate the optimal model size and number of tokens for training a transformer language model under a given compute budget. The authors train over 400 language models and find that for compute-optimal training, the model size and number of training tokens should scale at equal rates: for every doubling of model size, the number of training tokens should also be doubled. They train a 70B model called Chinchilla, compute-optimally according to their results, on 1.4 trillion tokens for a ratio of 20 tokens per parameter. For this reason, the scaling laws they propose are often called “Chinchilla scaling laws”.
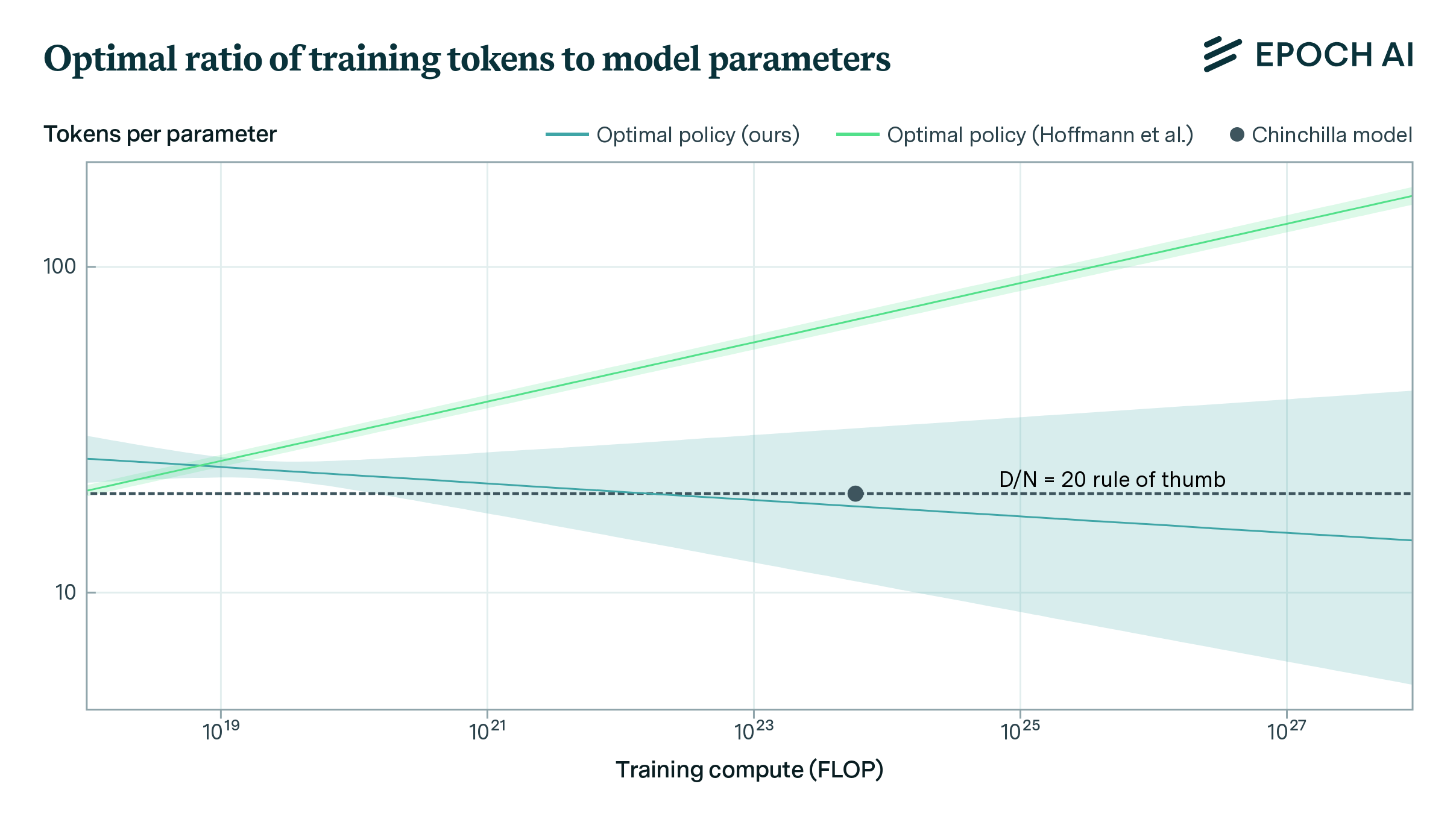
Figure 1: Optimal ratio of training tokens to model parameters using our estimates. Shaded regions represent 80% confidence intervals. While our estimates are consistent with the scaling policy used for Chinchilla, their estimates of their parametric model are not.
In their paper, Hoffmann et al. use three different methods to derive the optimal scaling policy. In one of their approaches, they estimate the following parametric scaling law:
\[L = E + \frac{A}{N^\alpha} + \frac{B}{D^\beta}\]which predicts how the cross-entropy loss L decreases as a function of the number of model parameters N and the number of training tokens D. This scaling law has been influential, and their estimates are commonly used in work on the topic, including our own.
We reconstruct a subset of the data in Hoffmann et al.’s paper by extracting it from their plots and fit the same parametric model. Our analysis reveals several potential issues with Hoffmann et al.’s estimates of the parameters of their scaling law:
- Hoffmann et al.’s estimated model fits the reconstructed data poorly, even when accounting for potential noise in the data reconstruction and excluding outlier models.
- The confidence intervals reported by Hoffmann et al. are implausibly tight given the likely number of data points they had (~400). Obtaining such tight intervals would require hundreds of thousands of observations.
- The scaling policy implied by Hoffmann et al.’s estimated model is inconsistent with their other approaches and the 20-tokens-per-parameter rule of thumb used to train their Chinchilla model.
In contrast, our parameter estimates (see equation below), which have higher values for the data-scaling exponent \(\beta\) and the irreducible loss \(E\), yield a model that fits the reconstructed data well and implies a scaling policy consistent with Hoffmann et al.’s other approaches and the token-to-parameter ratio used to train Chinchilla. Our work has implications for our understanding of the returns to additional scaling and the extent of our uncertainty about optimal scaling policies.
We have released a preprint describing our results. Our results can be reproduced using this Colab notebook, the reconstructed dataset from Hoffmann et al. can be found here, and the data reconstruction can be reproduced here.
Implications of this work
Previous work relied on Hoffmann et al.’s fitted estimates of Chinchilla’s parametric scaling law, including some work from Epoch. Our discovery suggests that many of these results may need to be revised.
We believe that the parametric scaling law (approach 3 in Hoffmann et al.’s paper) is the most useful and widely applicable of the scaling laws they presented. Unlike approaches 1 and 2, which are only applicable when training compute-optimal (or “Chinchilla optimal”) models, the parametric scaling law directly estimates the loss on a dataset for any choice of model size (N) and data (D). This makes it relevant in any situation where N and D are being chosen to optimize test loss.
To understand the utility of the parametric scaling law, consider that after training, large language models are generally put into production and served to users. To minimize inference costs, it is usually better to use a smaller model trained for longer than what is considered compute-optimal (at least in the sense of pre-training compute). The parametric scaling law can therefore help determine the optimal trade-off between model size and training time, given a budget for total inference and training costs.
This trade-off was illustrated by Sardana et al., who accounted for inference costs in building their own alternative to the Chinchilla scaling law. However, as they did not perform their own pre-training experiments, Sardana et al.’s work relied on the poorly fit version of the parametric scaling law from Hoffmann et al. Similarly, Faiz et al., used Hoffmann et al.’s fitted values to calculate the trade-off between carbon footprint during model training and test loss. Corrêa et al. used these fitted values to estimate the right size and training time of the small open source LLM they call TeenyTinyLlama.
Furthermore, the popular blog post chinchilla’s wild implications by nostalgebraist employed Hoffmann et al.’s fitted values to illustrate the idea that we might be “running out of data” to train larger language models.
This reliance on Hoffmann et al.’s values for the parametric scaling law is shared by some of Epoch’s own work too. For example, Epoch researchers used their values to upper bound the requisite compute to train models that can substitute for human researchers on R&D tasks. Additionally – similar to the approach in Sardana et al – Epoch researchers Pablo Villalobos and David Atkinson had previously used the estimates from Hoffmann et al. to analyze the trade-off between scaling models and reducing inference costs. David Owen had also cited these values when attempting to use model size and data size to predict LLM benchmark results.
Correcting this scaling law has therefore been a valuable exercise for improving Epoch’s own research, and may have implications beyond our work.
About the authors