What is the probability that the sun will rise tomorrow? What are the chances of a pandemic happening next year? What are the odds of survival of a new surgery that has been successfully executed only once?

These and many other questions can be answered appealing to a general rule: Laplace’s rule of succession. This rule describes the probability of a positive outcome given information about past successes. The versatility and generality of the rule makes it an invaluable tool to forecasters, who use it to estimate base rates¹.

Laplace’s rule can be stated in simple terms. If we have repeated an experiment \(T\) times, and observed \(S\) successes, we can estimate the posterior probability of obtaining a success in the next trial as \(p = \frac{S+1}{T+2}\). 

However, there is a fatal problem when applying the rule to observations over a time period, where the definition of what constitutes a trial is not as clear. For example, if we were to estimate the chances of a pandemic happening next year. Should we take \(T\) as the number of years that our dataset of past pandemics covers? Or as the number of days? This essentially arbitrary choice leads to different answers to our question².

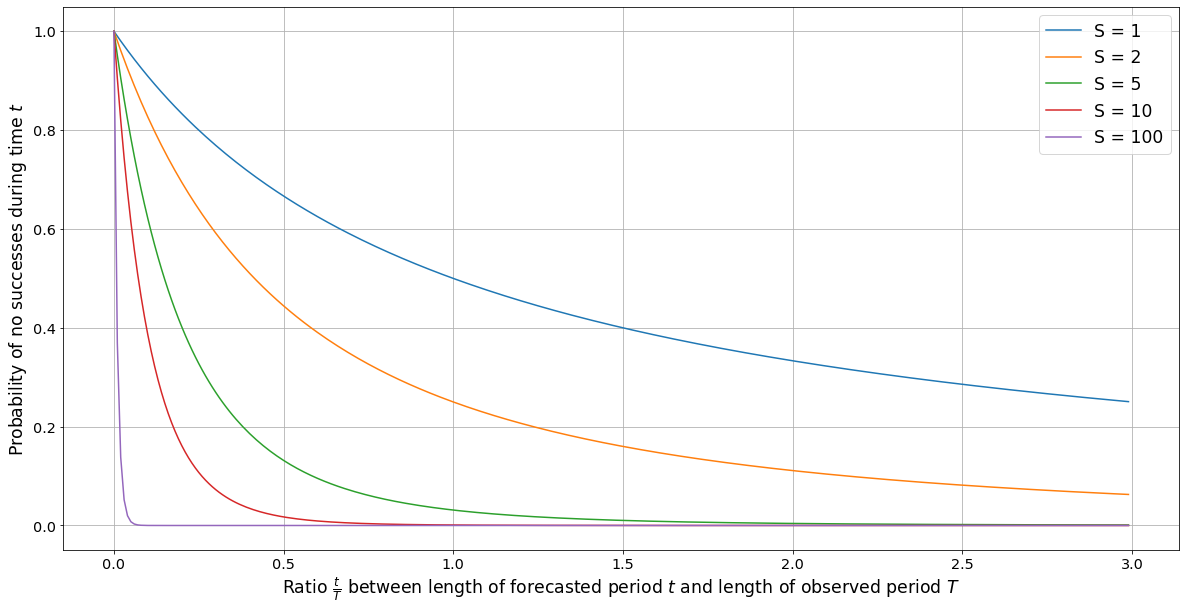
After grappling with this problem, our final recommendation is a simple formula. Essentially, if we have data on a time period of \(T\) years, and we have observed \(S\) successes over that period, the chances that no successes will happen in the next \(t\) years are \((1+\frac{t}{T})^{-(S+1)}\). We call this formula the time-invariant Laplace’s rule.

If we have chosen the observation period \(T\) so that it is equal to the time since the first recorded success, we will subtract one success from our count, and the probability ought to be instead \((1+\frac{t}{T})^{-S}\). This is because in this case we always expect the sampling period to have at least one success, so the first success provides us with no new information to update our prior on.

Number of observed successes S during time T	Probability of no successes during t time
\(S = 0\)	\((1+\frac{t}{T})^{-1}\)
\(S > 0\)	\((1+\frac{t}{T})^{-S}\) if the sampling time period is variable \((1+\frac{t}{T})^{-(S+1)}\) if the sampling time period is fixed

Graph showing values of the formula \((1+\frac{t}{T})^{-S}\) for various values of \(S\)

It’s important to note that this rule is recommended only as a replacement for Laplace’s rule and suffers from most of the same problems. In cases where Laplace’s rule is too aggressive because of its assumption of a virtual success, our time-invariant rule will also be too aggressive for the same reason. This problem becomes more pronounced the less evidence we’ve had to update on, so we should expect the rule to perform particularly poorly in cases when prior knowledge suggests the time until a success should be long but our observation period so far has been short.

In such cases a more careful analysis would try to integrate that information to the prior, for example as outlined in this article. In practice, approaches which take such information into account are superior, but they take us into the realm of semi-informative priors from the realm of uninformative priors, and this subject is outside the scope of our post.

This article is structured as follows: First, we will refresh Laplace’s rule of succession and how to apply it. Second, we will expose the time-inconsistency problem by way of an example. Third, we will explain how to fix it and derive a time-invariant version of Laplace’s rule. Fourth, we will illustrate the application of the time-invariant version of Laplace’s rule with an example. We conclude with a set of recommendations for forecasters.

Familiarity with Laplace´s rule of succession is recommended for this article. If you haven´t encountered Laplace´s rule before, we recommend you this past article by Ege Erdil to learn more.
 

A refresher: Laplace’s rule of succession 

Laplace’s rule of succession says that if we have observed S successes over T trials we should estimate the probability of success in the next trial as \(\frac{S+1}{T+2}\).

This is derived starting from a uniform prior on the probability of success per trial \(p \sim U(0,1)\), and applying a Bayesian update and taking the expected value of the result. We will not enter into the details of the derivation here, though we refer interested readers to this article.

Laplace’s rule of succession is often interpreted as introducing one virtual instance of success and one virtual instance of failure to our actual success and failure counts. This prevents us from reducing to \(0\) the probability of an event that has not happened before.

Laplace’s rule of succession can be applied successively to infer the probability that no successes will happen over the next \(t\) trials:

\[P(\text{No successes in $t$ attempts} | \text{$S$ successes in $T$ attempts}) = \\\]\[= P(\text{No success in attempt T+1} | \text{$S$ successes in $T$ attempts}) \cdots P(\text{No success in attempt T+t} | \text{$S$ successes in $T+t-1$ attempts}) =\]\[= (1 - \frac{S+1}{T+2}) \cdots (1-\frac{S+1}{T+t+1}) = \prod_{i=1}^{t}(1 - \frac{S+1}{T+i+1})\]

When expanding the chain, we have taken care of updating on the failures so far. Success becomes more and more unlikely the more time goes on without ever seeing it.
 

The problem of time

The problem with Laplace’s rule becomes apparent when we try applying it to a problem when there isn’t a clear definition of what constitutes a trial. Instead, we have observations of success gathered over a period of time.

Let’s suppose we are studying the likelihood of an earthquake. We have observed the seismograph of the Exampletopia region for a decade, and observed no earthquakes so far. The guild of architects of Exampletopia wants to know if the good luck will continue onto the next decade.

Ada the chief seismologist wastes no time in answering. We have seen no earthquakes over a decade. So by Laplace’s rule, the likelihood of no earthquakes happening in the next decade is \(1 - \frac{S+1}{N+2} = 1 - \frac{0+1}{1+2} = \frac{2}{3}\).

Byron the assistant seismologist takes a bit more time to answer. A decade is made of \(10\) years. So the likelihood of no earthquakes happening in the next 10 years, per our reasoning above, is:

\[(1 - \frac{S+1}{T+2}) \cdots (1-\frac{S+1}{T+t+1}) =\]\[= (1 - \frac{0+1}{10+2}) \cdots (1-\frac{0+1}{10+10+1}) =\]\[= \frac{11}{12} \frac{12}{13} \cdots \frac{19}{20}  \frac{20}{21} = \frac{11}{21}\]

The seismologists are getting different results!

Furthermore, these are not the only two possible results. had they divided the decade of observations into \(N\) periods, then they would have found a probability of no earthquakes happening equal to:

\[(1 - \frac{S+1}{T+2}) \cdots (1-\frac{S+1}{T+t+1}) =\]\[= (1 - \frac{0+1}{N+2}) \cdots (1-\frac{0+1}{N+N+1}) =\]\[= \frac{N+1}{N+2} \cdots \frac{2N}{2N+1} = \frac{N+1}{2N+1}\]

This result is absurd - the probability should not depend on how finely we subdivide the observations. Clearly Laplace’s rule cannot be applied naively in this setting. But what should we do instead?
 

A problem of priors

The reason the seismologists are getting different results is because they are starting from different priors for the probability of an earthquake.

Recall that Laplace´s rule is derived assuming a uniform distribution on the prior probability of the event of interest in each trial.

Ada defines each trial as a decade, so her prior probability (before taking into account the observations) of the chances of no earthquake over a decade (a single trial) is \(\frac{1}{2}\).

In contrast, Byron is working with years as his trial probability. The prior probability of no earthquakes for a decade from his point of view is \(\frac{1}{2} \frac{2}{3}\cdots \frac{10}{11} = \frac{1}{11}\).

No wonder their results are distinct! If you start from different assumptions it stands to reason that you will get different results.

This also suggests what we ought to do in order to fix the problem. We want a recipe to choose an (improper) prior that assigns the same probability of no earthquakes over any unit of time, no matter how finely you subdivide time.

But before we need to shift our perspective, from the discrete to the continuous. 
 

Continuous improvement

So far we have been thinking about Laplace’s rule in a discrete setting. We have a number of \(T\) discrete trials, and \(S\) of those result in successes. 

Instead, we want to take this process to the limit. We observe our process of interest over a continuous interval of time of length \(T\). And we observe \(S\) successes over that time.

The natural way to model the amount of occurrences that happen in an interval of time is a Poisson distribution. The Poisson distribution is parameterized by a rate parameter \(\lambda\), that represents the mean of events per unit of time we expect to observe.

Since we are observing the interval over \(T\) units of time, we model the number of observations we have seen so far as a \(\text{Poisson}(\lambda T)\).

This continuous setup encompasses all possible step lengths in the discrete one. We could recover the discrete setup defining binary variables that indicate if a success happened in a day, a month or a year. So we aren’t losing any flexibility by switching to the continuous setup³.

And when forecasting, we can vary the \(T\) variable to infer how likely is to observe a given quantity of successes over a period of arbitrary length. But before, we need to settle on a prior for \(\lambda\) and update it given the observations we have.
 

The scale invariant prior

Given that we want to do Bayesian inference, we have to pick some prior for \(\lambda\). How do we go about making this choice?

Suppose for the moment that the only fact we know about the arrival rate \(\lambda\) is that it’s an arrival rate and strictly greater than zero, though it could be arbitrarily close to zero. Since it’s an arrival rate, we know that it’s measured in units of time inverse, i.e. in units of frequency. So a particularly natural condition we could ask for in a state of total agnosticism about \(\lambda\) is that the prior distribution \(f(\lambda) \, d \lambda\) we assign to it does not change when we perform a change of time units.

In formal terms, we want to get the same answer when we do a change of units and then use \(f\) to get a prior as we would when we use \(f\) first and then do a change of units - we want the two operations to commute.

If this condition holds, we won’t have the problem we had with Laplace’s rule above. Regardless of how we end up subdividing the original interval we’ll always get the same prior distribution on \(\lambda\), and then performing a Bayesian update on it will always get us to the same posterior. It will be measured in different units, but this won’t affect any of the probabilities we calculate.

Let’s find which \(f\) makes this condition hold. Say that the two units of time we consider are related by a scaling constant \(1/c\), so that a unit change amounts to a substitution \(\lambda \to c \lambda_n\) - the subscript is used to denote that the right hand side is measured in the “new frequency unit”. If we get the prior first and then do a change of units, we’ll get \(c f(c \lambda_n) d \lambda_n\) as our probability measure. On the other hand, if we do a change of units first and then compute the prior, we’ll just get \(f(\lambda_n) d \lambda_n\). For these to be equal, we must have \(c f(c \lambda_n) = f(\lambda_n)\) for all \(c, \lambda_n > 0\), which implies that \(f(\lambda) \propto 1/\lambda\).⁴

There’s a problem with the scale-invariant prior \(f(\lambda) \, d\lambda = d\lambda/\lambda\): its integral over the whole positive reals is infinite, so though it defines a legitimate measure over the positive real numbers, this measure is not a probability measure. We can’t divide it by some finite constant to normalize it so that the total probability mass equals 1, as it must for a genuine probability distribution. This means it’s an improper prior. 

Even though improper priors are not normalizable, we can still use Bayes’ rule on them. In some cases, the posterior we get after some Bayesian updates can kill off their divergences that make them non-normalizable. In our case, these are the bad divergences the integral of \(d\lambda/\lambda\), or the natural logarithm, has at \(\lambda = 0, \, \infty\). Intuitively this is because given that we don’t know what units we’re measuring the arrival rate in, it can both be “very small” and “very large”. Unless the evidence we have excludes both possibilities, we will be unable to get any answers out of the scale-invariant prior.

Inference with the scale-invariant prior

Fortunately, the scale-invariant prior falls into the conjugate class of the Poisson likelihood. In particular, it can be expressed as a Gamma distribution with shape parameter \(\alpha=0\) and inverse-scale parameter \(\beta=0\).

This means that it is straightforward to update the distribution of  \(\lambda\) given the observed number of successes \(S\) and the length of observed time \(T\). The posterior distribution will be \(\lambda \sim \text{Gamma}(S, T)\). 

Then the amount of successes in the next \(t\) units of time is distributed as a Poisson with rate \(t \lambda\). The chances that no successes will be observed during this period are then:⁵

\[P(S’=0) = \int_0^\infty P(S’=0 | \lambda) f(\lambda) d\lambda = \int_0^\infty e^{-t\lambda} \frac{T^S}{\Gamma(S)} \lambda^{S-1}e^{-T\lambda} d\lambda = (1+\frac{t}{T})^{-S}\]

Summarizing, when we observe \(S\) successes over a period \(T\) of time, we recommend estimating the probability of no successes for an additional time t as \((1+\frac{t}{T})^{-S}\) ⁶. 
 

Unprecedented success

In the case where the observed number of success is equal to zero the formula we presented no longer works; we would get  the absurd result \(P(S’ = 0) = (1+\frac{t}{T})^{-S} = (1+\frac{t}{T})^0 = 1\).

This is because we have that the posterior distribution for \(\lambda\) is \(\text{Gamma}(0, T)\), whose PDF is \(f(\lambda) = \frac{T^S}{\Gamma(S)} \lambda^{S-1}e^{-T\lambda} = \lambda^{-1}e^{-T\lambda}\). This distribution is still not integrable, leading to the absurd result.

We have worked out two reasonable alternatives in this situation. One is to take the limit of the Laplace’s rule estimate as we divide time into \(N\to \infty\) parts. The second is to apply a weak version of Solomonoff induction . These approaches are worked out in appendices A and B, respectively.

Both alternatives lead to the same recommendation: if we have observed for a time \(T\), then the probability of seeing no successes during \(t\) extra time is \((1+\frac{t}{T})^{-1}\).

This result is astonishingly similar in form to the formula we worked out before. We can interpret it as adding one virtual success to make the prior integrable, as noted in the previous section. This echoes how a virtual success and a virtual failure are introduced in the standard form of Laplace’s rule⁷.

We were able to derive this formula in two different ways. And it shares structural similarity with the derivation starting from a scale invariant prior. Because of that, we are happy recommending it in the case where the number of successes is exactly zero.

However, this solution introduces an inconsistency. It leads to the formula giving the same result when \(S=0\) and when \(S=1\). To make the approach consistent in both cases, we recommend adding the virtual success in all cases. This will make forecasts made using the rule aggressive but no more so than ordinary Laplace.

As an important caveat, we want to underline that we get this result by artificially making low arrival rates unlikely by assuming a “virtual success” in some form, as stated above. This means in situations where we have good prior reasons to believe that a success is likely to take a long time, the rule is going to offer poor guidance. When the observation period becomes long enough that the strength of the evidence it implies is sufficient to swamp the prior, this is not a problem and the rule is safe to use.
 

Adjusting for a variable observation period

A common scenario in forecasting is that we have information about the first success, but no information about whether successes were possible before. For example, suppose that we want to get a base rate on pandemics that kill more than 3% of the global population. Wikipedia’s list for epidemics gives three such pandemics, the earliest being the Antonine Plague in the 2nd century. If we don’t know what was the time period for which we had good enough data to tell whether there was such a pandemic, then the best we can do is start our observation period with the earliest observation.

In this case we should not count the first success in the sampling period. This is because the first success does not contribute any term to the likelihood when we know it will always be there: the way we sample the data guarantees that our sampling period starts with a success, so the existence of a success gives us no additional information beyond success being possible. An event of probability 1 carries no information and hence we can’t do a Bayesian update on the basis of it occurring, which is why we ignore the first success when our sampling period is by construction anchored to a success at its start ^{8 9}.

In sum, when we adjust the time period T to exactly encompass S successes, we recommend estimating the probability of no successes over \(t\) time as \((1+\frac{t}{T})^{-S}\), again with the inclusion of a virtual success to ensure proper behavior when \(S = 1\).

Putting it all together

At this point we have put forward a practical suggestion to solve the problem of time invariance and two pitfalls to take into account when applying it.

We can summarize our recommendation in a table:

Number of observed successes S during time T	Probability of no successes during t time
\(S = 0\)	\((1+\frac{t}{T})^{-1}\)
\(S > 0\)	\((1+\frac{t}{T})^{-S}\) if the sampling time period is variable \((1+\frac{t}{T})^{-(S+1)}\) if the sampling time period is fixed

As a reminder, the sampling time period is variable iff you deliberately chose the observation period \(T\) to encompass the first success in your data. 

Let’s see our recommendation in practice.

An example: Earthquakes in Chile

Let’s say we want to forecast the probability that there will be an earthquake in Chile with a magnitude \(\geq 8\) this decade, so before start-of-year 2030.

First, let’s say we only know the date of the last such earthquake and we don’t know anything else. Wikipedia says that the last such earthquake was in September 2015 - let’s say this was exactly 7 years ago for simplicity. Since the time remaining from now until the start of 2030 is around 7.5 years, we can apply our formula in the case of one success with variable time and get the probability as

\[1 - \frac{1}{1+t/T} = 1 - \frac{1}{1 + 7.5/7} = 51.7 \%\]

Now, let’s suppose we know the dates of the last three earthquakes meeting the criterion and we want to use the scale-invariant prior approach. These are:

1. September 2015
2. April 2014
3. February 2010

We could of course just use the rule above and arrive at an answer, but instead we’ll do this example from first principles to demonstrate where the rule actually comes from.

If the earthquakes follow a Poisson process, then we can compute the likelihood for a given arrival rate \(\lambda\) by looking at the time gaps.¹⁰ Again, for simplicity we’ll round all time gaps to the nearest full year. This gives:

\[= \lambda e^{-4 \lambda} \times \lambda e^{-\lambda} \times e^{-7 \lambda}\]

Each factor corresponds to one of the time gaps: the (2)-(3) time gap, the (1)-(2) time gap and the time gap between (1) and today respectively. Bayesian updating on the scale-invariant prior \(d\lambda/\lambda\) therefore gives the posterior distribution

\[\sim \lambda e^{-12 \lambda} \, d \lambda\]

Now, if we want to compute the probability of no such earthquake in the next 7.5 years, we end up with

\[= \frac{\int_0^{\infty} \lambda e^{-(12 + 7.5) \lambda} \, d\lambda}{\int_0^{\infty} \lambda e^{-12 \lambda} \, d\lambda}\]

Here, the denominator normalizes the overall probability density defined by \(\lambda e^{-12 \lambda} \, d \lambda\) so that it actually integrates to 1, and the numerator is integrating the probability density against the likelihood \(e^{-7.5 \lambda}\) of not observing another earthquake for 7.5 years conditional on the value of \(\lambda\). In other words, this expression is marginalizing out \(\lambda\) using its posterior distribution.

It’s a general result that

\[\int_0^{\infty} \lambda^n e^{-t \lambda} \, d\lambda = t^{-n-1} \Gamma(n+1)\]

for \(t > 0, n \geq 0\) which we can plug into the above expression to get the final answer 

\[= \frac{19.5^{-1-1} \Gamma(1+1)}{12^{-1-1} \Gamma(1+1)}= \left( \frac{12}{19.5} \right)^2 = 37.8 \%\]

for the probability that there won’t be such an earthquake, or \(62.2 \%\) that there will be. 

Using Laplace’s rule at a timescale of months would have given us \(p \sim \operatorname{Beta}(1+2, 1+146) = \operatorname{Beta}(3, 147)\) for the posterior on the monthly success probability and

\[= \frac{\int_{0}^1 p^2 (1-p)^{146 + 90} \, dp}{\int_{0}^1 p^2 (1-p)^{146} \, dp} = \frac{B(3, 237)}{B(3, 147)} = 24 \%\]

for the probability that we see no earthquakes in the next 7.5 years, i.e. until the end of 2030. This is considerably smaller than the more conservative 37.8% given by the scale-invariant prior. The difference is because unlike the Laplace prior, the scale-invariant prior puts a lot of probability mass on small arrival rates, and here the evidence is not yet strong enough for this to be outweighed by the likelihood.

Finally, let’s take a much larger dataset and look at what happens to the discrepancy when we have a lot of evidence. The 14th last recorded earthquake of a magnitude of 8 or above in Chile happened in 1906. The scale-invariant prior therefore gives us a probability

\[\left( \frac{2022.5 - 1906}{2030 - 1906} \right)^{14 - 1} = 44.4 \%\]

that there won’t be another such earthquake until the start of 2030, or 55.6% that there will be. Instead, applying Laplace’s rule formally as above on an annual timescale gives

\[= \frac{\int_{0}^1 p^{13} (1-p)^{102 + 7.5} \, dp}{\int_{0}^1 p^{13} (1-p)^{102} \, dp} = \frac{B(14, 110.5)}{B(14, 103)} = 39.5 \%\]

In this case most forecasting rules are going to give similar answers¹¹, though our recommendation is still to use the scale-invariant prior unless you have some domain-specific reason to suspect it’s not a good prior to use. In most cases it will be better than using Laplace’s rule, and only slightly less convenient to compute.

Conclusion

Laplace’s rule is an essential tool to estimate base rates when forecasting.

In this article we have explained how we can extend it to the case where we observe a number of successes \(S\) over a continuous period of time \(T\).

The naive approach of subdividing \(T\) into a number of trials does not behave as we would like. However, we can estimate the probability of no successes happening during an additional \(t\) time as \((1+\frac{t}{T})^{-S}\).

We derive this formula from modelling the observations as the result of a Poisson process with a rate \(\lambda\). This rate is assumed to have the scale-invariant prior distribution \(f(\lambda) = 1/\lambda\). 

We have explained how to circumvent two pitfalls with this approach. When the number of successes is \(S=0\), we recommend adding one virtual success to our success count. And when we pick the time period \(T\) to exactly encompass the last \(S\) successes we recommend subtracting one success from the count.

Number of observed successes \(S\) during time \(T\)	Probability of no successes during \(t\) time
\(S=0\)	\((1+\frac{t}{T})^{-1}\)
\(S > 0\)	\((1+\frac{t}{T})^{-S}\) if the sampling time period is variable \((1+\frac{t}{T})^{-S-1}\) if the sampling time period is fixed

Three caveats are in order:

1. As the number of successes grows, the difference between the time-invariant rule and a naive application of Laplace’s rule becomes less significant. As a guide, for \(S \ge 3\) the results ought to be similar.
2. For small observation periods \(T \to 0\) we have that \((1+\frac{t}{T})^{-S}\to 0\). This rule is not appropriate when the observation period is much smaller than the forecasted period i.e. \(T \ll t\).
3. This rule applies when we don’t account for any extra information. For a more precise analysis, we recommend using background information to choose a better prior to start updating from. Tom Davidson covers this approach here.

The mechanical application of the rule we propose is no substitute for careful analysis and forecasting experience. Nevertheless, we still champion it as a useful and well-motivated rule of thumb.

Acknowledgements

We thank Eric Neyman, Jonas Moss, Tom Davidson, Misha Yagudin, Ryan Beck, Nuño Sempere and Tamay Besiroglu for discussion.

Anson Ho brought my (Jaime’s) attention to the time inconsistency of Laplace’s rule, and his research inspired this piece.

Eric Neyman proposed the idea of taking the limit of Laplace’s rule as we divide more finely the time. We develop this idea in appendix A.

Appendix A: Taking the limit

Credit goes to Eric Neyman for this idea

There’s a way to overcome the arbitrariness of choosing a time scale at which to apply Laplace’s rule by taking a limit instead. 

We work with the following setup: there are two states of the world \(F\) (failure) and \(S\)(success), and we’ve so far been in state \(F\) for an amount of time equal to \(T\). Without loss of generality we may choose our unit of time such that \(T=1\). Ideally we want to describe a probability distribution over \(t\) where \(t\) is the amount of additional time, denoted by \(Y\), we spend before we transition to state \(S\) for the first time. Note that we know \(t\) is greater than or equal to \(0\). We will characterize this distribution by its survival function \(s\). Recall that the survival function \(s(t)\) is defined as \(s(t) = \mathbb P(Y \geq t)\).

To do this, we subdivide our initial time interval into \(N\) pieces, or equivalently we partition time with a mesh equal to \(1/N\). If we use Laplace’s rule, then we start with a prior of \(p_{N} \sim \operatorname{Beta}(1, 1)\) over the transition probability \(F \to S\) per unit time, and we end up with a posterior of \(p_{\Delta t} \sim \operatorname{Beta}(1, N+1)\). The probability of observing no successes for an additional time \( t \geq 0\) is then

\[s_N(t) = \frac{1}{B(1, 1+N)} \int_0^1 (1-p)^{N(1+t)} \, dp = \frac{B(1, 1 + N(1+t))}{B(1, 1+N)}\]

because we’re integrating the probability of no success \( p^{Nt} \) with respect to the posterior distribution. We can express the beta function in terms of the gamma function and simplify this to get

\[s_N(t) = \frac{\Gamma(N+2) \Gamma(1 + N(1+t))}{\Gamma(2 + N(1+t)) \Gamma(N+1)} = \frac{N+1}{2 + N(1+t)}\]

Now, we take the limit as \(N \to \infty\), or as our partition of the initial interval becomes infinitely refined. We get the final result

\[s(t) = \lim_{N \to \infty} s_N(1+t) = \frac{1}{1+t}\]

when \(t \geq 0\). This regularization scheme therefore gives a well defined probability distribution over the arrival time of the next success without requiring the introduction of an arbitrary time scale.
 

Appendix B: Solomonoff induction

Applying Solomonoff induction to this setup is problematic mainly because we don’t make observations in discrete bits. However, we can remedy this problem by a discretization scheme, and then take a limit.

We’ll use a very weak and restricted version of Solomonoff induction: focus only on programs which output \(0\) for \(k\) steps before outputting \(1\) forever. The programs are therefore encoded directly by the value of \(k\) itself, represented in binary. We assume that we know there will eventually be an output of \(1\), an assumption also made by all succession rules. If we don’t make this assumption then Solomonoff induction gives more and more weight to the constant \(0\) program as the number of zeroes we have observed goes to infinity.

A standard prefix-free encoding of these programs would correspond to a prior \(\sim 1/k^2\) for the program that outputs \(k\) zeroes and then starts to output ones. If we suppose we observe \(N\) zeroes, the probability of observing at least \(fN\) more zeroes is roughly

\[\approx \int_{(1+f)N}^{\infty} \frac{dx}{x^2} \bigg/ \int_N^{\infty} \frac{dx}{x^2} = \frac{1}{1+f}\]

If we let \(N \to \infty\) then the approximation error made by replacing discrete sums with integrals goes to zero so this becomes the exact answer. In other words, if we know that a success is possible, then a naive approximation of Solomonoff induction gives the same answer as the regularization of Laplace’s rule given in appendix A.

On the other hand, without further information it’s impossible to glean from this how likely success being possible actually is - this is because without further information about what’s generating failures and successes, all nonzero and finite time intervals are equivalent from our perspective. Solomonoff induction breaks this symmetry by working explicitly with bit sequences, and in this case there is an obvious scale introduced by the number of bits seen so far, but there’s no such scaling that comes along if we’re in a continuous setup instead of a discrete one.

Appendix C: Previous work

We are not the first people to grapple with the question of time-invariance in Laplace’s rule setting. Here we cover two alternatives: semi informative priors and a natural unit approach.

In his Semi-informative priors over AI timelines, Tom Davidson thinks about how to fix the time invariance. He opts for choosing a prior Beta distribution for the probability of success that results in a given probability of success over the first year, and a number of virtual successes equal to 1.

His approach relies on using information on previous reference classes to pick what this first trial probability ought to be.

The choice of the number of virtual successes is less well motivated. Tom argues that as long as the first trial probability is small then many choices of virtual successes lead to similar results. In his article he opts to mostly work with a number of virtual successes equal to 1 for convenience.

Tom has written a separate piece outlining the key parts of his reasoning about Laplace’s rule here.

Jonas Moss explains how to shift between time units to choose a prior. 

In general, he suggests that if we believe that the natural unit is M (e.g. days), we want to work at the timescale M’ (e.g. hours), then the prior distribution for the M’ timescale is π’ = π^M’/M for π~B(1,1), which results in a π’ ~ B(M’/M,1) induced prior.

Of course, this whole approach relies on choosing a unit to impose a uniform distribution on.

Though reasonable, both approaches rely on complex choices. The semi informative priors approach in particular strikes us as a solid choice when background information from reference classes is available (though we would want to see a more rigorous treatment of the choice of number of virtual successes).

Nevertheless, we feel that a more mechanical approach like the one we propose in this articles has some advantages over these approaches. Chiefly, it allows you to quickly elicit an estimate without engrossing yourself in complex choices.

---

1. For example, see this forecast by Samotsvety in which Laplace´s rule of succession is used to estimate the chances of  a nuclear exchange between Russia and NATO. ↩

2. See appendix C for a summary of previous work. ↩

3. Modulo some problems when an interval spans more than one success. But we can solve this problems by subdividing time finely enough that this won’t happen. ↩

4. It’s also easy to see this by other methods, for instance by using dimensional analysis. We explicitly write out this calculation so people unfamiliar with these other methods can follow the argument. ↩

5. To expand on this derivation, start with the integral

   \(\)\(\int_0^\infty e^{-t\lambda} \frac{T^S}{\Gamma(S)} \lambda^{S-1}e^{-T\lambda} d\lambda\)

   Substituting \(u = (t+T) \lambda\) gives

   \(= T^S (t+T)^{-S} \int_0^\infty e^{-u} \frac{1}{\Gamma(S)} u^{S-1} \, du\)

   and the integral is equal to 1 by the definition of the Gamma function: it just amounts to computing \(\Gamma(S)/\Gamma(S)\). Therefore the final answer is

   \(= (1 + t/T)^{-S}\) ↩

6. Note that as \(T \to 0\) we have that \((1+\frac{t}{T})^{-S} \to 0\). This suggests that the formula is not appropriate when the observation time is very small compared to the horizon of our forecast. ↩

7. Even more on point, in standard Laplace’s rule we could have chosen to start from the improper and arguably less informative prior \(\text{Beta}(0,0)\). 

   But then if we observed \(T\) trials and \(S=0\) successes we would end with a posterior \(\text{Beta}(0,T)\), which is not proper.

   This is eerily similar to how in the time-invariant case we need to introduce a virtual success to make the result integrate properly.   ↩

8. Note that this is also the case with regular Laplace’s rule. ↩

9. There are some caveats here about whether you should make an anthropic update on the basis of your distance to the last success or not. In practice, assuming an additional success in this formalism has the same effect as doing an anthropic update under the assumption that the observer is equally likely to make an observation at any point in time. So if you think such an update is called for it’s not difficult to make. ↩

10. This is because if we’ve seen \(S\) events at times \(T_1, T_2, \ldots, T_S \) in a fixed time interval \(T\), we can compute the likelihood \(\mathbb P(T_1, T_2, \ldots, T_S \vert \lambda)\) by factorizing it as

    \[= \mathbb P(T_1 \vert \lambda) \times \mathbb P(T_2 \vert T_1, \lambda) \times \ldots \times \mathbb P(T_S \vert T_{S-1}, \lambda) \times \mathbb P(T_{S+1} > T \vert T_S, \lambda)\]

    using the memorylessness of a Poisson process. As the arrival time \(T_k\) is always exponentially distributed conditional on the arrival time \(T_{k-1}\), we can substitute out all these conditional probabilities using the probability density and the cumulative distribution function of an exponential distribution with arrival rate \(\lambda\). ↩

11. We could also have approximated the answer we get from Laplace’s rule by just assuming the posterior distribution of the annual success chance \(p\) is a Dirac delta distribution at the expected value \((13 + 1)/(115 + 2) = 12 \%\) and use this directly to deduce the chance of no success in \(7.5\) years as \((1-p)^{7.5} = 38.3 \%\) - almost the same answer as above since the posterior of \(p\) has most of its probability mass in a narrow region around its maximum. ↩